It's both my off day and Christmas. I could post an old race report. Or, I could just post nothing. But, I thought that I'd reflect a bit on Christmas, itself. I haven't made many theological posts to this blog. (BTW, I'm taking a full week off from blogging so I have more time to study, next post will be on New Years Day).
Of course, one does well to remember that such things are called mysteries of the faith for a reason. Anybody who claims to truly understand why an all-knowing and all-powerful god would be remotely interested in hanging around with bunch of moderately intelligent mammals is, well, full of it. The only easy way around the question is to say it's irrelevant because the whole religion is bogus. However, even atheists should acknowledge that it's at least an interesting thought experiment.
Anyway, mathematicians are used to dealing with things we don't really understand, so the absence of a satisfying answer isn't really a big problem.
First, let's start by putting some bounds around the question: Why would God become one of us?
Did he also become one of other groups on other planets (or other universes)? Is the incarnation through Mary the only way that he truly experienced the human condition or did he also get it vicariously through other prophets preaching other religions? Good questions, but we can't go after everything at once. Let's stick to the script as it's written and assume for the moment that this was the singular event of connection between God and mortals. Let's also dispense with the liberal view that Jesus wasn't really God with a capital G, but a person who was so enlightened that they were in full unity with god. That view is also an interesting one, but it makes Christmas pretty irrelevant. Christmas only matters if Christ was, in fact, God. The God.
The simple answer is that he loves us. A lot. OK, but that rather begs the question. Unless you can also explain why he loves us so much, you haven't really provided an answer. But, it does at least move us to more familiar ground. None of us can become a kitten, no matter how much we might want to commune with cats. But, we can understand how someone could love cats so much that they would do so if they could. I think we'd still call that individual a nut job, but it's comprehensible.
We're told that God loves us as a parent. I think that's a great metaphor and it certainly explains the willingness to make otherwise insane sacrifices, but I'm having a bit of a problem understanding why God would create a creature so limited and then regard it as offspring. We breed animals all the time and they are much closer to our capabilities than we are to God's but, despite the claims of a few overly zealous pet owners, we don't really think they are our children. We might be willing to risk death saving them from a burning building, but to become one of them, to give up our advantage as human and live as them and fully experience their suffering of death so as to redeem them from their erroneous ways? Get serious. Nobody would do that, even if they could.
But there might be something there.
Then again, this might be completely heretical. But I'll throw it out there anyway. If God calls me on it, I'll just be honest and admit that I'm speculating about things I can't possibly understand.
What if God saw this not just as something for us, but a growth opportunity for God as well? Loving relationships are supposed to work that way, right? Sure, you sacrifice for the one you love but, you also try to do it in a way that makes both of you stronger.
God had been watching this whole human experience thing unfold for a while (yes, yes, God's not bound by time, I'm writing in human-comprehensible terms). The worst of humanity was clear. But, so was the best. And the best is almost always connected to sacrifice. The standard view is that God instigated sacrifice as a means of atonement. Scripture certainly supports that view, but I don't believe it mandates it. Suppose sacrifice is actually something we cooked up?
When parents discipline their children, the kids do not regard it as sacrifice. They regard it as punishment. Sacrifice is when the kid voluntarily does something they otherwise wouldn't because they want to mend the relationship. If you're not too heavy handed with them, little kids actually do this quite a lot. The relationship really does matter to them. As parents, we sacrifice all the time as well we should - we signed up for the job and only the greatest fools think that such responsibility carries no cost.
God doesn't have to sacrifice. He's all powerful, remember? What if, God wanted in on this sacrifice thing because he saw how much better we are when we do it?
It's still a pretty nutty explanation but perhaps one worth pondering.
Sunday, December 25, 2016
Saturday, December 24, 2016
Fisher Information
It may start to look like all of statistics was invented by Ronald Fisher. If one is talking about frequentist statistics, that would not be too far from the truth. Just as Newton did with Calculus, Fisher took a field that wasn't going anywhere for reasons of intractability and figured out how to make it useful by focusing on a tighter problem and leaving the nasty edge cases for others. Now that computational resources exists to get around a lot of the thorny problems of open-form solutions, the work of Bayes and Laplace who preceded Fisher are gaining traction. But, back to Fisher.
As with most experimenters, Fisher was less interested in "truth" and more interested in making good decisions based on data. Others could work out why genetics (his primary field) operated the way it did, he was more interested in how to make it happen. Also common to most experimenters, Fisher had to deal with budget constraints. So, the obvious question: how do I get the most usable information for my money?
The idea that some estimators are better than others is obvious enough. Even little kids quickly figure out that just because a baseball player strikes out once, it doesn't mean they can't hit a ball. You have to see at least a few at bats to know that. But, once you're past that, you still have all sorts of estimators of ability. Should you look at batting average, slugging percentage, on base percentage, runs batted in, home run total, or (yes, people actually track these things) how often the opposing manager calls for a pitching change when this batter comes up?
Well, a big part of the problem with baseball stats is that nobody can agree on what they are actually trying to estimate. "Ability" is a pretty vague term. However, if you can actually quantify a parameter, then Fisher does have a pretty good technique for determining how well a statistic estimates that parameter. And, it's named after him: Fisher Information.
![I(\theta)=\textrm{E}\left[\left(\frac{\partial}{\partial\theta}\log f_\theta(X)\right )^2 |\theta \right ] =\int\left(\frac{\partial}{\partial\theta}\log f_\theta(X) \right )^2 f_\theta(x)\textrm{d}x](https://latex.codecogs.com/gif.latex?I(\theta)=\textrm{E}\left[\left(\frac{\partial}{\partial\theta}\log&space;f_\theta(X)\right&space;)^2&space;|\theta&space;\right&space;]&space;=\int\left(\frac{\partial}{\partial\theta}\log&space;f_\theta(X)&space;\right&space;)^2&space;f_\theta(x)\textrm{d}x)
It's probably not intuitively obvious what that quantity is telling us, so let's break it up into pieces.
First, we have f(X). That's the probability density of X for a given θ. Taking the log gives two nice properties. The first is that the information becomes additive. That is, the information from two random variables is twice the information from one. The second is that, under reasonable regularity conditions (there he goes again, just chucking the theoretical messy stuff to get something that works for every real world case you can imagine), the expectation of the first moment (also called the score) is zero.
A consequence of the latter property is that the second moment (that is, the Fisher Information) is equal to the variance of the score. So, what the Fisher Information is really measuring is the variance of the density function conditioned on the observation. If the variance is high, that means that the value of the observation will move the density function around quite a bit. If the variance is low, that means that the observation doesn't do much to inform our belief about θ. Well, OK, Fisher was a frequentist, so I'll put it in those terms: the variance tells us how much we should adjust our estimate based on the data.
If the density is twice differentiable, this becomes more obvious. In that case, you can decompose the second moment to get:
![I(\theta)=-\textrm{E}\left[\frac{\partial^2}{\partial\theta^2}\log f_\theta(X) |\theta \right ]](https://latex.codecogs.com/gif.latex?I(\theta)=-\textrm{E}\left[\frac{\partial^2}{\partial\theta^2}\log&space;f_\theta(X)&space;|\theta&space;\right&space;])
That is, the Fisher Information is the negative expectation of the second derivative of the support curve at the maximum likelihood estimated of θ. A steep negative second derivative means that the support drops off very quickly on both sides of the maximum likelihood value. That is, the maximum likelihood is a lot more than any other likelihood.
Applied to random variables, this is little more than a mathematical curiosity. However, because of the additive property, it also means that we can apply it to linear combinations of independent observations. That is helpful and it tells us how much marginal information we get when we increase sample sizes or use alternative metrics to estimate a parameter (for example, the median rather than the mean).
As with most experimenters, Fisher was less interested in "truth" and more interested in making good decisions based on data. Others could work out why genetics (his primary field) operated the way it did, he was more interested in how to make it happen. Also common to most experimenters, Fisher had to deal with budget constraints. So, the obvious question: how do I get the most usable information for my money?
The idea that some estimators are better than others is obvious enough. Even little kids quickly figure out that just because a baseball player strikes out once, it doesn't mean they can't hit a ball. You have to see at least a few at bats to know that. But, once you're past that, you still have all sorts of estimators of ability. Should you look at batting average, slugging percentage, on base percentage, runs batted in, home run total, or (yes, people actually track these things) how often the opposing manager calls for a pitching change when this batter comes up?
Well, a big part of the problem with baseball stats is that nobody can agree on what they are actually trying to estimate. "Ability" is a pretty vague term. However, if you can actually quantify a parameter, then Fisher does have a pretty good technique for determining how well a statistic estimates that parameter. And, it's named after him: Fisher Information.
It's probably not intuitively obvious what that quantity is telling us, so let's break it up into pieces.
First, we have f(X). That's the probability density of X for a given θ. Taking the log gives two nice properties. The first is that the information becomes additive. That is, the information from two random variables is twice the information from one. The second is that, under reasonable regularity conditions (there he goes again, just chucking the theoretical messy stuff to get something that works for every real world case you can imagine), the expectation of the first moment (also called the score) is zero.
A consequence of the latter property is that the second moment (that is, the Fisher Information) is equal to the variance of the score. So, what the Fisher Information is really measuring is the variance of the density function conditioned on the observation. If the variance is high, that means that the value of the observation will move the density function around quite a bit. If the variance is low, that means that the observation doesn't do much to inform our belief about θ. Well, OK, Fisher was a frequentist, so I'll put it in those terms: the variance tells us how much we should adjust our estimate based on the data.
If the density is twice differentiable, this becomes more obvious. In that case, you can decompose the second moment to get:
That is, the Fisher Information is the negative expectation of the second derivative of the support curve at the maximum likelihood estimated of θ. A steep negative second derivative means that the support drops off very quickly on both sides of the maximum likelihood value. That is, the maximum likelihood is a lot more than any other likelihood.
Applied to random variables, this is little more than a mathematical curiosity. However, because of the additive property, it also means that we can apply it to linear combinations of independent observations. That is helpful and it tells us how much marginal information we get when we increase sample sizes or use alternative metrics to estimate a parameter (for example, the median rather than the mean).
Friday, December 23, 2016
Lehmann–Scheffé theorem
Suppose we don't just want a "really good" estimator of a parameter. Suppose we want the "best". There are several ways to quantify that. One of the most common is the Minimum Variance Unbiased Estimator (MVUE). That is, the estimate with a distribution that has a mean equal to the true value and a lower variance than the distribution of any other estimate with a mean equal to the true value.
The first thing we can observe from that characterization is that we are firmly back in frequentist land with this whole notion of the "true value" of the parameter. That said, the Bayesians have an equivalent structure, the Bayes Estimator, the which minimizes a loss function applied to the posterior distribution and, if that loss function happens to be the usual mean squared error, you wind up with pretty much the same thing. So, onward without philosophical debate.
How do we know when we have a MVUE? (Just to throw further ambiguity on that question, some authors call it a UMVUE, the leading "U" standing form "Uniformly".) Well, we need yet another definition.
A complete statistic, S, for parameter θ is one where, for every measurable function g such that E(g(S(X|θ))) = 0 for all θ, P(g(S(X|θ)) = 0) = 1 for all θ.
Wowsers. What's that all about? Well, let's step back from the trees and try to see the forest for a bit. Recall that a minimal sufficient statistic can be written as a function of any other sufficient statistic. What completeness is saying is that this statistic is so "full" of information about the parameter, that the only way to get rid of that information is to run it through a function that forces everything to zero. Why zero? Well, that helps with verification since a lot of times you wind up with intractable integrals in the expectation where all you can say is, "It comes out to something other than zero." All the rest of it is just mathematical formality to catch weird edge cases on sets of measure zero and the like.
Not that it matters much in practice, but for MVUE's, we can actually relax this to bounded complete statistics, where you only have to show the condition holds if g is bounded except on a set of measure zero.
You may have guessed that you have to work pretty hard to cook up a statistic that is minimally sufficient and not bounded complete. You'd be right. But, having defended against such nonsense, we can now move on to the result, the Lehmann-Scheffé Theorem:
Finally, the omission of the "minimal" condition on the statistic is not an oversight. Any statistic that is both complete and sufficient is also minimally sufficient.
The first thing we can observe from that characterization is that we are firmly back in frequentist land with this whole notion of the "true value" of the parameter. That said, the Bayesians have an equivalent structure, the Bayes Estimator, the which minimizes a loss function applied to the posterior distribution and, if that loss function happens to be the usual mean squared error, you wind up with pretty much the same thing. So, onward without philosophical debate.
How do we know when we have a MVUE? (Just to throw further ambiguity on that question, some authors call it a UMVUE, the leading "U" standing form "Uniformly".) Well, we need yet another definition.
A complete statistic, S, for parameter θ is one where, for every measurable function g such that E(g(S(X|θ))) = 0 for all θ, P(g(S(X|θ)) = 0) = 1 for all θ.
Wowsers. What's that all about? Well, let's step back from the trees and try to see the forest for a bit. Recall that a minimal sufficient statistic can be written as a function of any other sufficient statistic. What completeness is saying is that this statistic is so "full" of information about the parameter, that the only way to get rid of that information is to run it through a function that forces everything to zero. Why zero? Well, that helps with verification since a lot of times you wind up with intractable integrals in the expectation where all you can say is, "It comes out to something other than zero." All the rest of it is just mathematical formality to catch weird edge cases on sets of measure zero and the like.
Not that it matters much in practice, but for MVUE's, we can actually relax this to bounded complete statistics, where you only have to show the condition holds if g is bounded except on a set of measure zero.
You may have guessed that you have to work pretty hard to cook up a statistic that is minimally sufficient and not bounded complete. You'd be right. But, having defended against such nonsense, we can now move on to the result, the Lehmann-Scheffé Theorem:
If S is a bounded complete, sufficient statistic for θ and E(g(S(X)) = τ(θ), then g(S(X)) is a MVUE for τ(θ).Don't get thrown off by the g and τ; they are just there to indicate that it's OK to run both the estimate and the parameter through further transformations. In particular, it's totally cool to come up with a statistic that meets all the criteria except for bias and then transform it to get rid of the bias.
Finally, the omission of the "minimal" condition on the statistic is not an oversight. Any statistic that is both complete and sufficient is also minimally sufficient.
Thursday, December 22, 2016
Rao-Blackwell Theorem
In my past posts on sufficient statistics, I've indicated my preference for the Bayesian formulation, so I'm sticking with that here, even though the frequentist version is more likely to appear on the Q. They are for all intents and purposes equivalent except in some weird infinite-dimension cases that I'm not too worried about. I'm also going to be somewhat informal on my definitions.
As previously noted a statistic is any function T of a random sample X. Preferably, the dimension of T(X) is less than that of X, but that's not a requirement; it just makes the statistic more useful since the whole point is data reduction.
A sufficient statistic for parameter θ is one such that P(θ|X) = P(θ|T(X)). And, from the Factorization Theorem (which, incidentally is also referred to as the Fisher-Neyman Factorization Theorem because all statistical results sound more legit if you attach Fisher's name to them), this is equivalent to saying the pmf/pdf, f, can be factored such that f(x|θ) = g(x)h(T(x)|θ).
A minimal sufficient statistic for parameter θ is a sufficient statistic that can be expressed as a function of any other sufficient statistic. In other words, any sufficient statistic can be further "boiled down" via another function to the minimal sufficient statistic. As functions never add information, the minimal statistic is the statistic where removing any more information results in the statistic becoming insufficient. Due to some nutty edge cases, you can't simply say that a minimal sufficient statistic has the minimum dimension of all sufficient statistics, but that is the gist of it.
Since there are infinitely many such sufficient statistics, it's impossible to verify directly that every sufficient statistic can be transformed to a candidate for minimal sufficient statistic. the Factorization Theorem is again useful. If S and T are both sufficient statistics, then f(x|θ) = g(x)h(T(x)|θ) = q(x)r(S(x)|θ). If S(x) = S'(T(x)) then the only part of the f that depends on θ is r(S'(T(x)|θ)). Since this must hold for any sufficient T(x) and corresponding S'(T(x)), we get the following equivalence: S(X) is a minimal sufficient statistic if and only if
}{f(\mathbf{y}|\theta)}\textrm{&space;independent&space;of&space;}\theta\Leftrightarrow&space;S(x)=S(y))
This is much easier to prove.
Having defined our terms, it's time to get to the result, which is actually very useful; the Rao-Blackwell Theorem:
As previously noted a statistic is any function T of a random sample X. Preferably, the dimension of T(X) is less than that of X, but that's not a requirement; it just makes the statistic more useful since the whole point is data reduction.
A sufficient statistic for parameter θ is one such that P(θ|X) = P(θ|T(X)). And, from the Factorization Theorem (which, incidentally is also referred to as the Fisher-Neyman Factorization Theorem because all statistical results sound more legit if you attach Fisher's name to them), this is equivalent to saying the pmf/pdf, f, can be factored such that f(x|θ) = g(x)h(T(x)|θ).
A minimal sufficient statistic for parameter θ is a sufficient statistic that can be expressed as a function of any other sufficient statistic. In other words, any sufficient statistic can be further "boiled down" via another function to the minimal sufficient statistic. As functions never add information, the minimal statistic is the statistic where removing any more information results in the statistic becoming insufficient. Due to some nutty edge cases, you can't simply say that a minimal sufficient statistic has the minimum dimension of all sufficient statistics, but that is the gist of it.
Since there are infinitely many such sufficient statistics, it's impossible to verify directly that every sufficient statistic can be transformed to a candidate for minimal sufficient statistic. the Factorization Theorem is again useful. If S and T are both sufficient statistics, then f(x|θ) = g(x)h(T(x)|θ) = q(x)r(S(x)|θ). If S(x) = S'(T(x)) then the only part of the f that depends on θ is r(S'(T(x)|θ)). Since this must hold for any sufficient T(x) and corresponding S'(T(x)), we get the following equivalence: S(X) is a minimal sufficient statistic if and only if
This is much easier to prove.
Having defined our terms, it's time to get to the result, which is actually very useful; the Rao-Blackwell Theorem:
If g(X) is an estimator of θ and S(X) is a sufficient statistic for θ, then E(g(X)|S(X)) is a generally better and never a worse estimator of θ. (By "better", we mean that the estimator has a lower expected mean squared error).Thus, you can start with pretty much any estimator and compute the conditional expectation to get a really good estimator. If you're using a minimal sufficient statistic, you get the added bonus of knowing the dimensionality of your inputs is minimized.
Wednesday, December 21, 2016
4.0v3.0
Grades were published today. I'm not sure how you get anything other than an "A" in a directed readings course, but it's still nice to see the streak go through my third term.
Tuesday, December 20, 2016
Factorization Theorem
Before getting to the named result, a word on sufficient statistics. I've already weighed in on my own biases, but I'm somewhat intrigued by the fact that the whole notion of sufficient statistics breaks down so quickly once one leaves the comfy realms of exponential distributions. It's no wonder frequentists love them so much. Of course, we Bayesians are often pinged for using distributions that form convenient conjugate priors rather than what best models the underlying data. It's really not a question of right or wrong; it's using the tool that works given your point of view. Just as a Baptist would quote the bible while a Nihilist would quote Nietzche; you go with what fits.
Anyway, assuming we do care about sufficient statistics and aren't assuming a distribution from the exponential family, how do we find one? The Factorization Theorem helps.
Consider, for example, the uniform distribution. Suppose you know that values are evenly distributed, but you have no idea what the upper bound is. It seems pretty obvious that the maximum value from your sample would be the best predictor of that and one could prove that from the definition of sufficient statistic. However, it's super easy if you use the Factorization Theorem:
f(x|θ) = 1/θ for 0 < x < θ so the joint distribution is f(x|θ) = θ-n for all 0 < xi < θ. Note that this density only depends on the minimum being greater than zero and the maximum being less than θ.
So, the only part of the distribution that depends on both x and θ can be re-written as a function of T(x) = max{xi} and θ. At this point, it should be fairly clear that you're done, but if you absolutely must grind it out, it goes like this:
T(x) = max{xi}
g(t|θ) = θ-n if t < θ
h(x) = 1
and
f(x|θ) = g(max{xi}|θ) = g(T(x)|θ)h(x)
Anyway, assuming we do care about sufficient statistics and aren't assuming a distribution from the exponential family, how do we find one? The Factorization Theorem helps.
Let f(x|θ) denote the joint pdf or pmf of a sample X. A statistic T(X) is a sufficient statistic for θ if and only if there exists functions g(t|θ) and h(x) such that, for all sample points x and all parameter points θ, f(x|θ) = g(T(x)|θ)h(x).As is so often the case with these characterization theorems, the proof is a less than enlightening exercise in symbol manipulation. So, we'll skip that. The result, on the other hand, does make it a whole lot easier to find a sufficient statistic, particularly when one steps outside the family of exponential distributions.
Consider, for example, the uniform distribution. Suppose you know that values are evenly distributed, but you have no idea what the upper bound is. It seems pretty obvious that the maximum value from your sample would be the best predictor of that and one could prove that from the definition of sufficient statistic. However, it's super easy if you use the Factorization Theorem:
f(x|θ) = 1/θ for 0 < x < θ so the joint distribution is f(x|θ) = θ-n for all 0 < xi < θ. Note that this density only depends on the minimum being greater than zero and the maximum being less than θ.
So, the only part of the distribution that depends on both x and θ can be re-written as a function of T(x) = max{xi} and θ. At this point, it should be fairly clear that you're done, but if you absolutely must grind it out, it goes like this:
T(x) = max{xi}
g(t|θ) = θ-n if t < θ
h(x) = 1
and
f(x|θ) = g(max{xi}|θ) = g(T(x)|θ)h(x)
Monday, December 19, 2016
Bad grammar
I don't have that much longer to finish my catalog of named results for the Q (not to mention that I need to actually study these results, not just write about them). However, I'm going to burn another day's post with a comment about notation. It comes from a generalization of Chebychev's Inequality.
Since it's a named result (though not one I've found much use for), I'll start by stating it in it's usual form:
If X is a random variable from a distribution with mean μ and variance σ2, then P(|X ‑ μ| ≥ kσ) ≤ k‑2.
OK, great. Now consider a random sample from the same distribution: X1, ..., Xn. Suppose we don't know what μ and σ2 are. What can we say about the bound using just the sample mean and standard deviation? Well, get ready...
\le\frac{1}{n+1}g\left(\frac{n(n+1)k^2}{n-1+(n+1)k^2}\right))
So far, just another messy formula but, it gets better. What's g?
=&space;\begin{Bmatrix}&space;\nu&space;&\qquad\textrm{if&space;}&space;\nu&space;\textrm{&space;is&space;even}&space;\\&space;\nu&space;&\qquad\textrm{if&space;}&space;\nu&space;\textrm{&space;is&space;odd&space;and&space;}t<a\\&space;\nu-1&space;&\qquad\textrm{if&space;}&space;\nu&space;\textrm{&space;is&space;odd&space;and&space;}t>a\\&space;\end{matrix})
Ummm, OK, you have a function of t and the answer in terms of ν and a. Oh, yeah, don't stress about that; they're both functions of t:
/t&space;\\&space;\\&space;a&space;&=&&space;\frac{(n+1)(n+1-\nu)}{1+\nu(n+1-\nu)}&space;\end{align*})
Oh, that's right, they're also a functions of n WHICH ISN'T ANYWHERE TO BE FOUND IN THE PARAMETER LIST. That's nuts. I'm not going to spend a lot of time trying to come up with a better way to express a result that I don't care about, but there simply has to be something better than that.
Since it's a named result (though not one I've found much use for), I'll start by stating it in it's usual form:
If X is a random variable from a distribution with mean μ and variance σ2, then P(|X ‑ μ| ≥ kσ) ≤ k‑2.
OK, great. Now consider a random sample from the same distribution: X1, ..., Xn. Suppose we don't know what μ and σ2 are. What can we say about the bound using just the sample mean and standard deviation? Well, get ready...
So far, just another messy formula but, it gets better. What's g?
Ummm, OK, you have a function of t and the answer in terms of ν and a. Oh, yeah, don't stress about that; they're both functions of t:
Oh, that's right, they're also a functions of n WHICH ISN'T ANYWHERE TO BE FOUND IN THE PARAMETER LIST. That's nuts. I'm not going to spend a lot of time trying to come up with a better way to express a result that I don't care about, but there simply has to be something better than that.
Sunday, December 18, 2016
Pere Marquette 2016
Run December 10, 2016.
I had my cry. I had it a year ago when I crossed the finish line at Pere Marquette. It wasn't a terrible run by any means. But, it wasn't what I had done before. And, at my age, the decline is typically permanent.
Since then, I've been trying to get myself to a point where I can enjoy the event without worrying about the result. That attitude ended up resulting in a couple of pretty decent results in the spring (Woodlands, Double Chubb) where relaxing in the first half of the race allowed me to find some push in the second. But, by summer, the residual fitness was wearing off quickly. I struggled through the Silver Rush 50, running my worst time for the distance by over an hour. By Mark Twain, I was toast. It was time to do some serious re-evaluation. It wasn't enough to pretend I didn't care; I would always care. I had to redefine what it meant to succeed.
Yes, yes, I'll get to the race report in a minute. Indulge me a diversion.
When Yaya was five, she won her first orienteering meet. When she was eight, she won her first national championship (US Primary School Orienteering Championships). Then, she quit. "It's just not my thing," she said. Obviously, it was her thing, but what she didn't want was to turn into me. She didn't want to be someone who was always expected to do well. She wanted to just do whatever she was doing and let the result be what it was. Between the national coaching staff taking an interest, constant attention at local meets, and, of course, me, that just wasn't going to happen. So, she quit.
I think I get that. But, I probably don't. It's just not the way I'm wired.
Which brings us to the starting line of Pere Marquette in 2016 (told you I'd get there). And the question is not can I win (I already know the answer to that one) but can I even do this in a way that isn't completely depressing? Can I find some meaning in the effort independent of the result? If I can't, there really isn't much point in coming here every year. On yet another tangent; this is my 16th entry at Pere Marquette, which moves it out of a tie with the Possum Trot as my most attended race ever (not counting weekly training-race type things).
Wave zero is called to the line. Yes, that includes me, wearing bib #14. The top 25 runners shuffle up. It's pretty hard to say you don't care when you're toeing the line with some of the best trail runners in the midwest. At exactly 9:30AM, we get the gun. For the next 15 minutes, another 25 runners will start every 30 seconds. Wave 1 contains the top 15 women and ten more fast guys. The next 10 (or so) waves contain runners who have been seeded based on results in this event from the preceding three years. After that are the waves of runners who have indicated potential, but have yet to prove it on Pere Marquette's tortured slopes. Finally, a few waves of folks who openly admit that they are just happy to complete the course.
After a couple hundred meters of flat, we hit the first of four major climbs. The first climb is actually three short steep climbs punctuated by two short level sections. I go right to the back of the wave on the first ascent. This always happens; I don't like taking the first climb out too hard. What's different is that I don't move up many spots on the level section heading into "The Squeeze". The Squeeze is a narrow crack through a rock face that forces the field to go single file. That's no big deal in wave zero, since six minutes of running is plenty of time to string things out. For later waves, it can be a bottleneck.
On the second part of the climb, I do manage to pass a couple people, but I'm very aware that I'm pushing much harder than I usually would. On the next level section, I compose myself and try to focus only on my own effort. That's not easy to do as the top 2 over-50 runners (Rick Barnes and Dan Rooney) are still in sight about 30 seconds up the trail. I forcibly remove them from my thoughts. Run your own race. Breathe, push, stride.
By the top of the climb, the fastest wave 1 runners have caught me. This is clearly going to be the year I get kicked out of wave zero. In some ways, that's a relief. If I'm not in wave zero next year, I'll be able to just kick back, not get up at 6AM for my pre-run, eat the big breakfast buffet at the Lodge, and not have to worry about defending a seed I can't possibly live up to. But, this year, I'm still in wave zero. There's no shame in losing, but there's plenty in not trying. I know how to descend technical trails. I crank it up and, while I only pass one runner, I open a pretty good gap to those behind.
That leaves the little matter of the second climb, which is quite steep. However, I've always run this one well and this year turns out not to be the exception. Then comes half an hour of meandering trail with lots of little obstacles, but nothing to break your stride if you run it right. By the base of the third climb, I'm pretty much on my own.
The third climb is similar to the second, except that you're half an hour more tired so the grade really hurts. I run the whole thing, passing three people who have decided to walk it. One of them, Chad Silker - who I know quite well from the SLUGs, takes one look at me passing him and decides that he needs to be moving faster (he's right, even at my best, I rarely beat him; of course, he has a 3-month-old at home, so he's probably not been too focused on running lately). He blows by me just past the summit and stretches it out on the descent.
The fourth climb at Pere Marquette truly is the stuff of legends. It's not that big, a little over 100m tall, but at 3/4 of the way in, it comes right when a properly run race is really starting to hurt. The first few hundred meters are a stiff grade. Then it gets crazy steep. Then, even that isn't enough, so they built steps. Not just normal stadium-style steps that you might do repeats on. Crazy, weird-spaced steps made from whatever stones happened to be nearby. Some steps are 6" high, others over a foot. It's pretty much the death knell to any rhythm you were trying to carry into the last few minutes of the race.
This is the sort of obstacle where experience counts as much as fitness. I've run these steps enough times that I know how to do it without losing my stride. It would probably be just as fast to walk them, but by running them, I get right back on my pace at the top. Then comes the long descent to the finish (which is really just running back down the first climb). I try to keep a good turnover, and do a pretty good job of getting through The Squeeze quickly, but I still get caught right at the bottom. There's nothing I can do about it; I have no legs left for a 200m sprint to the line. I finish as firm as I can.
I'm 22nd across the line, but a couple more from later waves have better elapsed times to put me in 24th overall; 3rd in my age group (oh crap, top 25, they might still put me in wave zero next year). While my time is rather slow compared to previous results, it's a respectable 1:01:47. Objectively, it's a pretty good result. So, how to respond to the vexing question that will be asked dozens of times over the next hour at the post-race party in the Lodge, "How did you do?"
The total jerk response would be to say I did terrible; that I used to be so much faster; that I just don't really put any effort into this sort of thing anymore. OK, I'm not quite that much of a jackass.
The completely insincere response would be, "Good!" No, this is the group of people with which I have the closest bond of experience. I have to do better than that.
It strikes me that the honest answer is perhaps also the best. "I gave it a good run. I'm happy."
I had my cry. I had it a year ago when I crossed the finish line at Pere Marquette. It wasn't a terrible run by any means. But, it wasn't what I had done before. And, at my age, the decline is typically permanent.
Since then, I've been trying to get myself to a point where I can enjoy the event without worrying about the result. That attitude ended up resulting in a couple of pretty decent results in the spring (Woodlands, Double Chubb) where relaxing in the first half of the race allowed me to find some push in the second. But, by summer, the residual fitness was wearing off quickly. I struggled through the Silver Rush 50, running my worst time for the distance by over an hour. By Mark Twain, I was toast. It was time to do some serious re-evaluation. It wasn't enough to pretend I didn't care; I would always care. I had to redefine what it meant to succeed.
Yes, yes, I'll get to the race report in a minute. Indulge me a diversion.
When Yaya was five, she won her first orienteering meet. When she was eight, she won her first national championship (US Primary School Orienteering Championships). Then, she quit. "It's just not my thing," she said. Obviously, it was her thing, but what she didn't want was to turn into me. She didn't want to be someone who was always expected to do well. She wanted to just do whatever she was doing and let the result be what it was. Between the national coaching staff taking an interest, constant attention at local meets, and, of course, me, that just wasn't going to happen. So, she quit.
I think I get that. But, I probably don't. It's just not the way I'm wired.
Which brings us to the starting line of Pere Marquette in 2016 (told you I'd get there). And the question is not can I win (I already know the answer to that one) but can I even do this in a way that isn't completely depressing? Can I find some meaning in the effort independent of the result? If I can't, there really isn't much point in coming here every year. On yet another tangent; this is my 16th entry at Pere Marquette, which moves it out of a tie with the Possum Trot as my most attended race ever (not counting weekly training-race type things).
Wave zero is called to the line. Yes, that includes me, wearing bib #14. The top 25 runners shuffle up. It's pretty hard to say you don't care when you're toeing the line with some of the best trail runners in the midwest. At exactly 9:30AM, we get the gun. For the next 15 minutes, another 25 runners will start every 30 seconds. Wave 1 contains the top 15 women and ten more fast guys. The next 10 (or so) waves contain runners who have been seeded based on results in this event from the preceding three years. After that are the waves of runners who have indicated potential, but have yet to prove it on Pere Marquette's tortured slopes. Finally, a few waves of folks who openly admit that they are just happy to complete the course.
 |
| Top of first climb |
On the second part of the climb, I do manage to pass a couple people, but I'm very aware that I'm pushing much harder than I usually would. On the next level section, I compose myself and try to focus only on my own effort. That's not easy to do as the top 2 over-50 runners (Rick Barnes and Dan Rooney) are still in sight about 30 seconds up the trail. I forcibly remove them from my thoughts. Run your own race. Breathe, push, stride.
By the top of the climb, the fastest wave 1 runners have caught me. This is clearly going to be the year I get kicked out of wave zero. In some ways, that's a relief. If I'm not in wave zero next year, I'll be able to just kick back, not get up at 6AM for my pre-run, eat the big breakfast buffet at the Lodge, and not have to worry about defending a seed I can't possibly live up to. But, this year, I'm still in wave zero. There's no shame in losing, but there's plenty in not trying. I know how to descend technical trails. I crank it up and, while I only pass one runner, I open a pretty good gap to those behind.
 |
| The Steps on Climb 4 |
The third climb is similar to the second, except that you're half an hour more tired so the grade really hurts. I run the whole thing, passing three people who have decided to walk it. One of them, Chad Silker - who I know quite well from the SLUGs, takes one look at me passing him and decides that he needs to be moving faster (he's right, even at my best, I rarely beat him; of course, he has a 3-month-old at home, so he's probably not been too focused on running lately). He blows by me just past the summit and stretches it out on the descent.
The fourth climb at Pere Marquette truly is the stuff of legends. It's not that big, a little over 100m tall, but at 3/4 of the way in, it comes right when a properly run race is really starting to hurt. The first few hundred meters are a stiff grade. Then it gets crazy steep. Then, even that isn't enough, so they built steps. Not just normal stadium-style steps that you might do repeats on. Crazy, weird-spaced steps made from whatever stones happened to be nearby. Some steps are 6" high, others over a foot. It's pretty much the death knell to any rhythm you were trying to carry into the last few minutes of the race.
 |
| Descending below The Squeeze |
I'm 22nd across the line, but a couple more from later waves have better elapsed times to put me in 24th overall; 3rd in my age group (oh crap, top 25, they might still put me in wave zero next year). While my time is rather slow compared to previous results, it's a respectable 1:01:47. Objectively, it's a pretty good result. So, how to respond to the vexing question that will be asked dozens of times over the next hour at the post-race party in the Lodge, "How did you do?"
The total jerk response would be to say I did terrible; that I used to be so much faster; that I just don't really put any effort into this sort of thing anymore. OK, I'm not quite that much of a jackass.
The completely insincere response would be, "Good!" No, this is the group of people with which I have the closest bond of experience. I have to do better than that.
It strikes me that the honest answer is perhaps also the best. "I gave it a good run. I'm happy."
Friday, December 16, 2016
Where's the math at?
So, I've been thinking about how to get some more math into my research. I am, after all, getting a PhD in math (applied math, yes, but still math).
I poked around looking for some ideas:
I poked around looking for some ideas:
- Turns out, stable distributions, while possessing some really fine mathematical properties, are extrodinarily difficult to use in Bayesian analysis because their pdf's and are generally intractable, which makes computing posterior distributions really, really hard. As my measures come from fat-tailed stable distributions and I prefer to use Bayesian analysis, this is worth looking into.
- My problem of maximizing correlation within a block is best handled by a heuristic. The problem is most likely np-complete, and therefore not any algorithm isn't much use on a data set of any reasonable size; it would never finish. It would be nice, however, to be able to come up with some sort of bound as to how far off the heuristic is from optimal. The way to do this is to solve the same problem in what's known as the "dual space". The best non-technical description of the dual space is that it's the solution space turned inside-out. So the optimal solution in the problem space yields a converse solution in the dual space. For any sub-optimal solution, the difference between it and the optimal answer is always less than or equal to the difference between the solution and its dual. So, getting an approximation bound comes down to identifying the dual space and projecting the solution into that space. Unfortunately, Algebra isn't really my strong suit. Maybe it's worth addressing that just so I can pursue this line. (Maybe it's worth addressing that simply because math teachers really ought to know Algebra).
- For that matter, proving the problem is np-complete would be cool. It would certainly help justify all the hoops we're jumping through.
- As this is all time series data, it seems that there should be some way to leverage that. My adviser very much wants me to go down that road. I'm not exactly sure what's there. Sure, all these projections are based on actuarial models which could be reverse engineered, but that rather defeats the purpose. We ran them through the model because we wanted the time series; if all we wanted was the assumptions that generated the time series, we could just look them up directly. Still, from an estimation standpoint, all these series are very similar in the way they run off. That structure can be exploited.
- While I've been focusing mainly on cash flow projections for insurance policies (mainly because that's the data I have), there's probably some merit to generalizing this to any cash flow and looking at what assumptions matter and which ones can be relaxed.
- Warp statistics. Sorry Sabermetrics (baseball stats) nerds, I'm not talking about Wins Above Replacement Player. This is a method for transforming densities to make MCMC simulation converge. I'm not that terribly interested in MCMC techniques, except that whatever makes them converge also tends to make my sampler converge. There's some evidence, based on Warp transformations, that Stable distributions aren't really the best bet for financial modeling. OK, then what is? This one is wide open.
Anyway, the point is that the math is out there. It may not be the core of my research, but there's no reason I can't tie in some beefy math results along with my computational work.
Thursday, December 15, 2016
Way forward
I met with a member of the Computer Science faculty yesterday. She seemed a lot more interested in my topic than most folks I pitch it to. Her research (looking for genetic patterns in Alzheimer's patients) is only marginally related, but the techniques have some overlap. She agreed to critique my CISS paper. Just the fact that she understands working with high-dimensionality data makes her opinion useful. Compared to a DNA sequence, my set of 1000 attributes is quite tiny.
So, feeling somewhat better that this topic is not a dead end, I'm giving some thought to where the road might lead.
First, the practical problem we're trying to solve (there's no rule that says a PhD topic has to address a practical problem, but it's somewhat easier to stay on course if it does): we want to quickly retrieve sums of measures from a large data set with attribute values matching an arbitrary set of criteria. Important words here are "quickly", "large", and "arbitrary". The lack of quantification of these terms would prompt any competent Business Analyst to reject this as a statement of requirements. However, we're not really interested in requirements, we're interested in direction, so we'll leave them vague.
If pressed, I'd say sub-second response to a query involving a half dozen attributes (out of 1000 possible) applied to a trillion rows. My Hewlett Packard rep would read that and say, "Vertica already does that!" True, provided the data is sufficiently structured, the model is properly optimized, the criteria specifies a rectangular-solid region of the dimensional space, and I'm willing to write a check for a million dollars to cover hardware and software licenses. I'd like to relax at least a few of those constraints.
If pressed on that one, I'd say that any observation can have any collection of attributes or measures as long as they are present in the data dictionary and mean the same thing across all observations where they are present. I'd say that the model should optimize itself in response to usage. I'd say that the shape of the region can be pretty much any combination of unions and intersections, including non-contiguous value lists (I might even admit arbitrary convex hulls though I'd need to think about how that statement generalizes to un-ordered, categorical attributes). Finally, I'd say it should be hosted on open-source software running on a couple hundred grand worth of hardware (or some similar setup in the cloud that could be leased for a few thousand a month).
One of the reasons I'm being vague is that, when I present this in two years, all those criteria will sound silly because costs have come down so much. However, that won't make the problem less relevant. Data will expand by at least as much. Despite the huge decrease in unit costs over the last 50 years, companies spend more than ever on computation and storage. So, those are my feelings in "today's dollars", so to speak. Two years from now, I'll restate them, adjusted appropriately.
My thought going into all this was that the way to pull this off was to write a good sampler. The problem with "random" sampling a database is that "randomly" doing anything in a large database is really inefficient. You always want to be working on sets of rows, not individual entries. Ideally, your unit of work is the physical block, which typically contains a few thousand rows. Writing processing directly against the physical storage is feasible, but fraught with implementation details that don't translate from one host to another. So, the next best thing is usually the logical block. Either way, you're looking at groups of records that are typically very highly correlated. I figured that the trick would be to adjust for the correlation.
As it turns out, correlation is the least of my concerns. The bigger problem was that, whether sampled by block or row, the estimates of the sums didn't converge. Because the measures were from heavy-tailed distributions, you could be way off, even with 90% of the data sampled. So, I've spent the last 9 months developing CISS to deal with that problem. That's great, but it still leaves the larger question open. CISS is reasonably fast and it does give decent estimates but, in putting it together, it occurred to me that the same methods that create a good sampler also do a fair job of organizing the data for a full search.
So, that's where we're going. Rather than reduce correlation in blocks, I'm going to try to maximize it. In the process, I'll also tag blocks with descriptions of the attribute values that block represents. So far, this isn't much different than what a relational data base does with indices. The difference is that the "index" changes with each block. Some blocks might be identified by what office the data came from. Others might be identified by the client company. Others might have rows coming from a single product. The query engine then tries to determine which blocks contain the rows in question without actually reading the blocks. The goal is that, any time a block is actually read, it returns a lot of relevant rows.
Achieving that goal is the interesting part. As queries come in, the query engine records statistics on each block regarding how often it was excluded and how many rows it returned when it was included. Blocks that consistently return low row counts, get dumped and their data is re-allocated to the "good" blocks that remain. This process is repeated in the background indefinitely, causing the system to continuously tune itself to query patterns and new data coming in.
There's not quite as much math in all this as I'd like. I'm hoping that somewhere along this road there are some interesting theorems to prove. None are jumping out at me right now, but we'll see what we can come up with.
So, feeling somewhat better that this topic is not a dead end, I'm giving some thought to where the road might lead.
First, the practical problem we're trying to solve (there's no rule that says a PhD topic has to address a practical problem, but it's somewhat easier to stay on course if it does): we want to quickly retrieve sums of measures from a large data set with attribute values matching an arbitrary set of criteria. Important words here are "quickly", "large", and "arbitrary". The lack of quantification of these terms would prompt any competent Business Analyst to reject this as a statement of requirements. However, we're not really interested in requirements, we're interested in direction, so we'll leave them vague.
If pressed, I'd say sub-second response to a query involving a half dozen attributes (out of 1000 possible) applied to a trillion rows. My Hewlett Packard rep would read that and say, "Vertica already does that!" True, provided the data is sufficiently structured, the model is properly optimized, the criteria specifies a rectangular-solid region of the dimensional space, and I'm willing to write a check for a million dollars to cover hardware and software licenses. I'd like to relax at least a few of those constraints.
If pressed on that one, I'd say that any observation can have any collection of attributes or measures as long as they are present in the data dictionary and mean the same thing across all observations where they are present. I'd say that the model should optimize itself in response to usage. I'd say that the shape of the region can be pretty much any combination of unions and intersections, including non-contiguous value lists (I might even admit arbitrary convex hulls though I'd need to think about how that statement generalizes to un-ordered, categorical attributes). Finally, I'd say it should be hosted on open-source software running on a couple hundred grand worth of hardware (or some similar setup in the cloud that could be leased for a few thousand a month).
One of the reasons I'm being vague is that, when I present this in two years, all those criteria will sound silly because costs have come down so much. However, that won't make the problem less relevant. Data will expand by at least as much. Despite the huge decrease in unit costs over the last 50 years, companies spend more than ever on computation and storage. So, those are my feelings in "today's dollars", so to speak. Two years from now, I'll restate them, adjusted appropriately.
My thought going into all this was that the way to pull this off was to write a good sampler. The problem with "random" sampling a database is that "randomly" doing anything in a large database is really inefficient. You always want to be working on sets of rows, not individual entries. Ideally, your unit of work is the physical block, which typically contains a few thousand rows. Writing processing directly against the physical storage is feasible, but fraught with implementation details that don't translate from one host to another. So, the next best thing is usually the logical block. Either way, you're looking at groups of records that are typically very highly correlated. I figured that the trick would be to adjust for the correlation.
As it turns out, correlation is the least of my concerns. The bigger problem was that, whether sampled by block or row, the estimates of the sums didn't converge. Because the measures were from heavy-tailed distributions, you could be way off, even with 90% of the data sampled. So, I've spent the last 9 months developing CISS to deal with that problem. That's great, but it still leaves the larger question open. CISS is reasonably fast and it does give decent estimates but, in putting it together, it occurred to me that the same methods that create a good sampler also do a fair job of organizing the data for a full search.
So, that's where we're going. Rather than reduce correlation in blocks, I'm going to try to maximize it. In the process, I'll also tag blocks with descriptions of the attribute values that block represents. So far, this isn't much different than what a relational data base does with indices. The difference is that the "index" changes with each block. Some blocks might be identified by what office the data came from. Others might be identified by the client company. Others might have rows coming from a single product. The query engine then tries to determine which blocks contain the rows in question without actually reading the blocks. The goal is that, any time a block is actually read, it returns a lot of relevant rows.
Achieving that goal is the interesting part. As queries come in, the query engine records statistics on each block regarding how often it was excluded and how many rows it returned when it was included. Blocks that consistently return low row counts, get dumped and their data is re-allocated to the "good" blocks that remain. This process is repeated in the background indefinitely, causing the system to continuously tune itself to query patterns and new data coming in.
There's not quite as much math in all this as I'd like. I'm hoping that somewhere along this road there are some interesting theorems to prove. None are jumping out at me right now, but we'll see what we can come up with.
Wednesday, December 14, 2016
Done
CISS Paper is done.
Plan (the major initiative I support at work) is done.
Semester is done.
Fall racing season is done.
Port of our reporting at work to HDFS is done.
All of these have gone to done in the last week. Not surprisingly, I'm a bit tired.
There are, of course, some loose ends.
The CISS paper, will need revisions before publication. That's assuming, of course, it even sees publication. That's much less of a sure thing than I'd like, but that's another day's worry.
The Plan initiative will have a recalc sometime early next year which will entail losing a night's sleep to production support.
The HDFS platform is working great in the non-production environment. There's a whole bunch of monitoring and automation that needs to be put in place before this becomes a true production system.
But, I'm still done with all the big tasks that needed to get done this year, except...
The Q.
I really need to get that checked off my list. February 10 is the date.
Plan (the major initiative I support at work) is done.
Semester is done.
Fall racing season is done.
Port of our reporting at work to HDFS is done.
All of these have gone to done in the last week. Not surprisingly, I'm a bit tired.
There are, of course, some loose ends.
The CISS paper, will need revisions before publication. That's assuming, of course, it even sees publication. That's much less of a sure thing than I'd like, but that's another day's worry.
The Plan initiative will have a recalc sometime early next year which will entail losing a night's sleep to production support.
The HDFS platform is working great in the non-production environment. There's a whole bunch of monitoring and automation that needs to be put in place before this becomes a true production system.
But, I'm still done with all the big tasks that needed to get done this year, except...
The Q.
I really need to get that checked off my list. February 10 is the date.
Tuesday, December 13, 2016
Variance 4.0
I think this one might actually be the winner. First, the results. I expanded the vertical scale around the true answer to better show the convergence. The 95% bounds contain the real answer 97% of the time. (Bounds are colored red when they do not contain the answer). The only extended period outside the bounds is after a somewhat fluky block was sampled early on, throwing one of the stratum estimates off by quite a bit. But the time anybody would actually be accepting the result, any deviations from the bounds is quite minor.
So, what did I actually do? Well, as the Russians appear to be reading this blog again (really, a bunch of hits lately), I'll have to be a little vague; especially since my adviser doesn't seem to be in any hurry to get this published. But, basically, it's just subbing in the sample moments with a prior bias towards extremely variable results. It works, it's fast, and it parallelizes. Still some writing to do, but I'm callin' this one done.
So, what did I actually do? Well, as the Russians appear to be reading this blog again (really, a bunch of hits lately), I'll have to be a little vague; especially since my adviser doesn't seem to be in any hurry to get this published. But, basically, it's just subbing in the sample moments with a prior bias towards extremely variable results. It works, it's fast, and it parallelizes. Still some writing to do, but I'm callin' this one done.
Monday, December 12, 2016
Non parametric variance.
So, let's assume for a second that we have some sort of intractable distribution of blocksums (and the empirical data certainly support such an assumption). What to do? Well, after a bit of panicking that my entire paper had been undermined, it occurred to me that the silly little theorem I proved might actually be the thing that saves me.
Let's start by restating it:
Let X be a random variable with finite mean and variance having pdf f(x|λ), where λ is a real-valued vector of parameters from a prior distribution with finite mean such that E(X|λ) = g1(λ) and E(X2 |λ)= g2(λ). Let X' be a random variable such that X'~X with probability θ and X'=0 otherwise where θ~Beta(a,b). Then:
E(X') = μ = aE(g1(λ))/(a+b)
and
Var(X') = σ2 = (bμ2 + a[E(g2(λ)) - 2μE(g1(λ)) + μ2])/(a+b)
Nowhere in there do we claim to have any clue as to what f(x|λ) actually is. All we need are the moments of the distribution (g1 and g2). Ok, we don't know those, either, but we can certainly estimate them. While the sample moments are the minimum variance unbiased estimators, they are also very likely to mess up the computations because there's far too much chance of not getting any hits in the first few blocks and having everything collapse to zero. So, we need to use the parameter λ to drive the functions to converge to the sample moments (which, in turn, converge to the true moments), but not too quickly.
We've seen no reason to depart from B(a,b) as our prior for θ, so we'll stick with that. Since we know that the uniform assumption is a fairly safe upper bound on variability, that's a good place to start for g1(λ), g2(λ). That is, we'll define them in such a way that their respective expectations under the prior on λ are the first two moments of the uniform. We'll pick some convenient conjugate distribution on λ for moving that towards the sample moments as more block hits come in. This will bias us towards oversampling early, when an error on the low side would be bad because it makes us think we've got an answer when we really don't.
Yes, this is still parametric in the sense that the underlying prior on λ will obviously impact the results. However, I'm pretty sure that by the time we stop sampling, the posterior will be pretty free from prior affects.
Let's start by restating it:
Let X be a random variable with finite mean and variance having pdf f(x|λ), where λ is a real-valued vector of parameters from a prior distribution with finite mean such that E(X|λ) = g1(λ) and E(X2 |λ)= g2(λ). Let X' be a random variable such that X'~X with probability θ and X'=0 otherwise where θ~Beta(a,b). Then:
E(X') = μ = aE(g1(λ))/(a+b)
and
Var(X') = σ2 = (bμ2 + a[E(g2(λ)) - 2μE(g1(λ)) + μ2])/(a+b)
Nowhere in there do we claim to have any clue as to what f(x|λ) actually is. All we need are the moments of the distribution (g1 and g2). Ok, we don't know those, either, but we can certainly estimate them. While the sample moments are the minimum variance unbiased estimators, they are also very likely to mess up the computations because there's far too much chance of not getting any hits in the first few blocks and having everything collapse to zero. So, we need to use the parameter λ to drive the functions to converge to the sample moments (which, in turn, converge to the true moments), but not too quickly.
We've seen no reason to depart from B(a,b) as our prior for θ, so we'll stick with that. Since we know that the uniform assumption is a fairly safe upper bound on variability, that's a good place to start for g1(λ), g2(λ). That is, we'll define them in such a way that their respective expectations under the prior on λ are the first two moments of the uniform. We'll pick some convenient conjugate distribution on λ for moving that towards the sample moments as more block hits come in. This will bias us towards oversampling early, when an error on the low side would be bad because it makes us think we've got an answer when we really don't.
Yes, this is still parametric in the sense that the underlying prior on λ will obviously impact the results. However, I'm pretty sure that by the time we stop sampling, the posterior will be pretty free from prior affects.
Sunday, December 11, 2016
Still some work to do.
The distribution of this data is just nutty. The confidence bounds are still a bit too tight, so I plotted the distribution of the blocksums to see if the exponential assumption might be off. Here's one stratum:
I don't know what that is, but it sure isn't exponential. Since the stratification has already removed the heavy-tail problem, I have to assume that this is caused by correlation within blocks. The consequence is that my estimate of the blocksum variance is about 10% low. That's not a killer in and of itself, but when I start summing them all up and assuming normality on the sum, it winds up being off by a fair bit.
The algorithm isn't very useful if it's this sensitive to the distribution of blocksums. The whole point of going to blocksums rather than using the individual observations was to smooth things out. I may need to switch to a non-parametric distribution. Or, I might just use the actual sample variance and use a t-distribution on the sum instead of normal.
I'm uncovering questions faster than I'm answering them. As I'm trying to just get this result published so I can move on, that's not really where I want to be.
I don't know what that is, but it sure isn't exponential. Since the stratification has already removed the heavy-tail problem, I have to assume that this is caused by correlation within blocks. The consequence is that my estimate of the blocksum variance is about 10% low. That's not a killer in and of itself, but when I start summing them all up and assuming normality on the sum, it winds up being off by a fair bit.
The algorithm isn't very useful if it's this sensitive to the distribution of blocksums. The whole point of going to blocksums rather than using the individual observations was to smooth things out. I may need to switch to a non-parametric distribution. Or, I might just use the actual sample variance and use a t-distribution on the sum instead of normal.
I'm uncovering questions faster than I'm answering them. As I'm trying to just get this result published so I can move on, that's not really where I want to be.
Saturday, December 10, 2016
PMETR
Today I ran the Pere Marquette Endurance Trail Run for the 16th time. It was the 28th running of the event. For the last ten years, it's also been a little weekend getaway for our family. The race is run on the trails of Pere Marquette State Park in Grafton, IL (about an hour from St. Louis). We go up the evening before and stay at the lodge there.
While I could have wrecked that by bringing some studies with me, I moved my off day to Saturday again. I will write up a full report next weekend. For this week, I'll just note two things:
While I could have wrecked that by bringing some studies with me, I moved my off day to Saturday again. I will write up a full report next weekend. For this week, I'll just note two things:
- My fitness is really falling off in a hurry. Despite very good conditions, I was nearly 4 minutes off my time from a few years ago. And, this is a race where 4 minutes is A LOT. Despite the term "Endurance" in the name, it's a 1-hour effort; pretty much full on the whole way.
- Despite that, I'm still running well enough to enjoy these things. That's not to say I don't wish I could have run better (I do), just that I'm starting to accept where I am with less complaint.
Friday, December 9, 2016
Refactor
Astute readers may have noticed that the graph I originally posted yesterday demonstrated a bug in the CIS Sampler. Basically, the sampler was not properly ensuring that blocks were only sampled once; that is, it was sampling with replacement. While this is valid in general, the variance computation depends on knowing the number of unread blocks, so it was actually messing up the bounds. It was a fairly easy thing to fix but, in the process of fixing it, I realized that the overall structure of my code is not what it should be. I won't go into details; I'll just state that, if I'm going to make this code public (and I don't know why I wouldn't), I should probably refactor a few things so the object relationships are a bit more clear.
Some of this is the result of porting from C# to Java. I just copied a lot of the code across. I was rather surprised how well this worked; sure the two languages are siblings, sharing C++ as a parent, but I wouldn't have thought that something like three quarters of the statements would copy and compile without any modification at all. Anyway, the stuff that didn't copy was all the LINQ stuff since Java doesn't have comparable functional constructs. Splitting that out into imperative statements compromised the design a bit.
Mostly, though, I'd say it's lack of peer review. I'm used to throwing designs together really quickly at work and then letting the team comment on them. That seems to go faster than trying to get everything exactly right on the first try (and, doing a sort of good job, but still pulling the whole team into a review is the least efficient route). So, in absence of the peer review step, my design has some holes.
Fortunately, it all seems to work and I have a pretty good set of unit tests. Therefore, I should be able to change things around pretty freely and still be able to get it all functioning again quickly.
Some of this is the result of porting from C# to Java. I just copied a lot of the code across. I was rather surprised how well this worked; sure the two languages are siblings, sharing C++ as a parent, but I wouldn't have thought that something like three quarters of the statements would copy and compile without any modification at all. Anyway, the stuff that didn't copy was all the LINQ stuff since Java doesn't have comparable functional constructs. Splitting that out into imperative statements compromised the design a bit.
Mostly, though, I'd say it's lack of peer review. I'm used to throwing designs together really quickly at work and then letting the team comment on them. That seems to go faster than trying to get everything exactly right on the first try (and, doing a sort of good job, but still pulling the whole team into a review is the least efficient route). So, in absence of the peer review step, my design has some holes.
Fortunately, it all seems to work and I have a pretty good set of unit tests. Therefore, I should be able to change things around pretty freely and still be able to get it all functioning again quickly.
Thursday, December 8, 2016
Full data set
I've run the CISS algorithm on a full-sized production data set. The results aren't much different from what I was expecting, but I'm still glad I took the time to do it. Actually, "full-sized" is probably a stretch. This is a 480-million row data set reflecting 5-year cash flow projections. Any decent BI tool can handle that. However, it is a "complete" set, meaning that the distribution of measures should closely match the 60-billion row data set that motivated this problem. By 10% sampled, it's pretty close. By 20%, you basically have your answer.
If you think that using a complete data set made the heavy-tail problem go away, guess again. Here's the estimate convergence where blocks are selected randomly:
Even at 90% of the data read, it's way off. Note that I have matched the axis on these graphs, so there's no cheating going on. Also, in case it's not clear (which it probably isn't), the x-axis is the number of blocks read. I used 100,000 row blocks.
If you think that using a complete data set made the heavy-tail problem go away, guess again. Here's the estimate convergence where blocks are selected randomly:
Even at 90% of the data read, it's way off. Note that I have matched the axis on these graphs, so there's no cheating going on. Also, in case it's not clear (which it probably isn't), the x-axis is the number of blocks read. I used 100,000 row blocks.
Wednesday, December 7, 2016
Holy Grail
Today's colloquium was about using artificial intelligence to prove mathematical theorems. Automated Theorem Proving (ATP) has been one of those "Holy Grail" type quests for the AI community since the dawn of the genre. I don't use that term in the complementary form; more in the "fools errand" connotation (though that's certainly too strong). It seems like the perfect combination of noble, difficult, and achievable (well, I don't know that looking for the Holy Grail in England qualified on that last one, but a legend as durable as Arthur is allowed a little leeway). However, under closer inspection, it starts to look pointless, infeasible, and still really, really hard.
Pointless because theorem proving isn't really what drives mathematics. The applied folks (like me) really don't care that much. If something works empirically, we go with it. The theoretical folks do care, but, as all of theoretical mathematics is predicated on which axioms you accept, what is and isn't provable rests more on your point of view than any skill with logic.
Infeasible because mechanical rigor simply doesn't work in math (or anywhere else, for that matter). This comes as a surprise to many but serious mathematicians are well aware of the fact that the emperor has no clothes. Regardless of which axioms you come up with, there will be unprovable assertions (that is, statements that can be neither proven true or false). Worse, there will also be contradictions (statements that, while technically provable, are at direct odds with other statements that are provable).
Now, it's not like ATP has no value at all. The famous "four color" problem (you can color any map using only four colors without having contiguous regions use the same color) was solved via ATP and no human-readable version of the proof has followed. OK, that's great. Still, Rand McNally wasn't exactly stressing over having to reset their plates. Nobody had come up with a counterexample in 6,000 years of mapped history. Chances were pretty good that their 4-color press was adequate.
And, it's this last bit that (almost) makes me want to take a swing at the problem. What if, for just a second we relaxed the correctness criteria. That is, we didn't worry about whether the automatic proofs were correct, just whether they were "consistently correct". Maybe we even give a certainty rating. X=>Y. Y=>Z. Therefore, X=>Z. Yeah, you can take that one to the bank. No integer solutions to an + bn = cn where n > 2? Well, maybe we're not so sure about that, though it sure appears to be right.
My point is that math isn't about logic. Sure that's the tool you use just as vibrations in the air are the tool that a jazz musician uses. But, it's not what makes the field great. What makes it great is the intuitive leap; the grab at something that doesn't really exist. No ATP algorithm will ever get that. To get that, you have to leave the world of algorithms and move to heuristics. Things that are probably true. Or even things that may well not be true but are worth a shot anyway. There's no reason a computer can't process things like this. But it means accepting that they might be wrong. The ATP True Believers don't want to accept that. They want the clarity of math in the 1700's (which was actually a big jumbled mess and had to be completely rewritten in the ensuing 200 years; people just hadn't realized the limits of logic yet).
Anyway, my BIG IDEA for all this (which I am NOT going to pursue, so anybody who wants to run with it is more than welcome to do so without crediting me in the least) is to try a 2-stage process. The first step is the creator, which is an empirically-based logic engine that knows the general patterns of successful proof, but is willing to hop across gaps in the logic if that's what it takes. The second is the peer reviewer, that does what all good peer reviewers do: pokes holes in the proof and sends them back for further analysis. The creator then tries to bridge these (presumably smaller) gaps in the logic. If it succeeds, at least by its loose standards, it re-submits to the peer reviewer. If it fails, it tries the whole thing over again. This continues until both the creator and peer reviewer agree. Sound familiar? It should. It's been working in real life for around 600 freakin' years! Seriously, why is nobody doing this?
Pointless because theorem proving isn't really what drives mathematics. The applied folks (like me) really don't care that much. If something works empirically, we go with it. The theoretical folks do care, but, as all of theoretical mathematics is predicated on which axioms you accept, what is and isn't provable rests more on your point of view than any skill with logic.
Infeasible because mechanical rigor simply doesn't work in math (or anywhere else, for that matter). This comes as a surprise to many but serious mathematicians are well aware of the fact that the emperor has no clothes. Regardless of which axioms you come up with, there will be unprovable assertions (that is, statements that can be neither proven true or false). Worse, there will also be contradictions (statements that, while technically provable, are at direct odds with other statements that are provable).
Now, it's not like ATP has no value at all. The famous "four color" problem (you can color any map using only four colors without having contiguous regions use the same color) was solved via ATP and no human-readable version of the proof has followed. OK, that's great. Still, Rand McNally wasn't exactly stressing over having to reset their plates. Nobody had come up with a counterexample in 6,000 years of mapped history. Chances were pretty good that their 4-color press was adequate.
And, it's this last bit that (almost) makes me want to take a swing at the problem. What if, for just a second we relaxed the correctness criteria. That is, we didn't worry about whether the automatic proofs were correct, just whether they were "consistently correct". Maybe we even give a certainty rating. X=>Y. Y=>Z. Therefore, X=>Z. Yeah, you can take that one to the bank. No integer solutions to an + bn = cn where n > 2? Well, maybe we're not so sure about that, though it sure appears to be right.
My point is that math isn't about logic. Sure that's the tool you use just as vibrations in the air are the tool that a jazz musician uses. But, it's not what makes the field great. What makes it great is the intuitive leap; the grab at something that doesn't really exist. No ATP algorithm will ever get that. To get that, you have to leave the world of algorithms and move to heuristics. Things that are probably true. Or even things that may well not be true but are worth a shot anyway. There's no reason a computer can't process things like this. But it means accepting that they might be wrong. The ATP True Believers don't want to accept that. They want the clarity of math in the 1700's (which was actually a big jumbled mess and had to be completely rewritten in the ensuing 200 years; people just hadn't realized the limits of logic yet).
Anyway, my BIG IDEA for all this (which I am NOT going to pursue, so anybody who wants to run with it is more than welcome to do so without crediting me in the least) is to try a 2-stage process. The first step is the creator, which is an empirically-based logic engine that knows the general patterns of successful proof, but is willing to hop across gaps in the logic if that's what it takes. The second is the peer reviewer, that does what all good peer reviewers do: pokes holes in the proof and sends them back for further analysis. The creator then tries to bridge these (presumably smaller) gaps in the logic. If it succeeds, at least by its loose standards, it re-submits to the peer reviewer. If it fails, it tries the whole thing over again. This continues until both the creator and peer reviewer agree. Sound familiar? It should. It's been working in real life for around 600 freakin' years! Seriously, why is nobody doing this?
Tuesday, December 6, 2016
Somewhat warm molasses
OK, so here's a little tip for any newbie Java programmers: jdbc isn't particularly good at figuring stuff out. If you ask it for 480 million rows (as I just did) and don't tell it anything else, it fetches those rows one at a time. Yes, really. It's quite happy to fetch them 10,000 at a time if you suggest that. And, obviously, the latter strategy will be a lot faster, but you have to tell it.
My extract is still slower than I'd like, but at least it's run time is now on the order of magnitude I was expecting (it's pulling about a million rows a minute - I was hoping for twice that, but we're getting there).
My extract is still slower than I'd like, but at least it's run time is now on the order of magnitude I was expecting (it's pulling about a million rows a minute - I was hoping for twice that, but we're getting there).
Monday, December 5, 2016
Molasses
Well, the plan was to post about how great CISS was doing on a full-sized data set. Instead, I'm posting about how ridiculously slow jdbc is for getting stuff out of an Oracle database. You'd think the company that essentially owns Java would make it fast on their own database. You'd be wrong.
Saturday, December 3, 2016
2009 Castlewood 8 Hour
I decided to take my off day on Saturday this week. Last week, I checked the control locations for this year's Castlewood 8-Hour which is going on today. So, this week's off-day throwback race report is to the last time I competed in the event.
December 5, 2009
I've written before that the hardest part of Adventure Racing is putting the team together. I don't mean that as a joke, either. Adventure Racing is all about being reasonably good at a lot of things. Excellence is not required but, as David Frei likes to say, "You can't suck at anything." Almost anybody can learn this stuff, but it takes a LOT of time to learn it all. Finding others who are willing to spend the time (or better yet, have already spent the time) is really tough. So, when Yvonne Deyo agreed to team up for the Castlewood 8- Hour after a 5-year hiatus (during which she produced two children) that was cause for celebration regardless of the outcome.
But, expectations can be a tricky thing to manage. Yvonne's last Adventure Race was when she, David, and I took fourth at 2004 National Championships. At the time, she was widely regarded as one of the best female amateurs in the country. Her return has been the subject of continuous speculation and now that the day is at hand there are more than a few teams taking notice.
While she has done an excellent job of staying generally fit through two pregnancies, there's a big difference between being "in shape" and being ready for a race of this distance. Her situation is further compromised by the fact that she had recently injured her hamstring. While it held up the previous week at the St. Louis 3-hour orienteering meet (where she took the Women's title), she still has to be careful not to re-injure it.
So while we cheerfully tell each other that it is just great to be back racing together, the truth is we are both harboring a fair bit of pre-race anxiety. Her, because the crucible of competition often produces answers to questions you'd just as soon not have asked. And me because, let's be frank, my last outing (Berryman 36-hour in September) was an unmitigated disaster and, if I race like that here, she might just accept one of the dozens of standing offers to race on another team.
We are bused from Castlewood to the start at Greensfelder. It's a balmy 17F as we wait for the 7AM start. We're given our maps for the first section a few minutes before the start. We can take the first 11 controls in any order. Then there are a few more down to the bike exchange. Between nerves and the cold I'm shaking so badly I can hardly draw the lines to connect the control circles to indicate our route. Fortunately, the first thing we have to do is run a couple kilometers on road to where our punch cards are waiting. Even though we take it quite slow (no point in risking aggravating Yvonne's injury in the first 10 minutes of the race), it's enough that we both stop shivering.
We're pretty near the back of the field (and at 100 teams, it's a pretty big field for a regional race) when we leave the road to cut straight through the woods to the card pickup. Almost all the teams take the longer route on the road, but the road is so steep, the usual speed advantage isn't there. Plus, by climbing the steeper route, we can use the tow and make better progress up the hill. We end up being one of first teams into the pickup.
Now the real navigation starts. By orienteering standards, the controls would be considered a mix of intermediate and advanced. That puts them in the "Super Hard" category of Adventure Racing controls. Although the map we're using is old, it is a real orienteering map as opposed to the usual USGS quad. This all adds up to a big advantage for the teams like ours that have considerable orienteering experience.
Another such team is Alpine Shop. While we're technically not competing against them (they're in the 4-person division), as the #1 ranked team in the country, they provide a pretty good standard to measure by. They've all raced for Carol's Team at one point or another and we're all good friends, so when we meet them at the fifth control, I can't resist throwing a few taunts their way. Not to be outdone, they fire back just as quickly. Tempting as it is to lock horns with them in our favorite discipline, prudence dictates letting them go. Out game plan is "easy pace, no mistakes" and we have no idea what is in store for us after this initial section is done. Yvonne continues to use the tow on the climbs and we run at a steady, but conservative pace the rest of the time.
A couple controls later we get to one where the bag is hung from a tree growing out from a nearly vertical embankment. Getting to the control from above isn't particularly tough, but rather than slide down the embankment, I decide to climb back up. As I twist and grab another tree to swing back up to the top, my shoulder decides to pop out of the socket.
This isn't exactly a novel maneuver for my right shoulder. This is the third dislocation to match an equal number of separations. I let out enough of a yell that another team comes over to assist, but there really isn't much to be done. It appears our race is over. Then, as I move to get back up, it suddenly snaps back into the socket with an audible pop. Perhaps it's just in contrast to the pain that preceded, but it really feels OK. Yvonne looks for a cue and I just say, "Let's go."
We take it easy for a while since the footing on Greensfelder's steep ridges is spotty and a fall in this state could be disastrous. Still, the navigation is sufficiently technical that even at a slow pace, we're doing well by being accurate. Accurate enough, in fact, that we end up meeting Alpine Shop again. David is handling the maps as usual and he is despondent. This technical nav section was his chance to get them a clear lead but an error has set them back.
The optimal route through the controls seemed pretty obvious to me, and apparently David agreed as we are hitting them in the same order. However, there are certainly differences of opinion on that. At each control, teams are coming and going in all different directions, so it's very hard to know where we really stand. We hang with Alpine Shop for a couple legs, but they are clearly on a mission to get back in the lead and we have to let them go.
We arrive at the exchange area at 8:45. While it's obvious from the nearly 300 bikes lying around that we're doing well, that's as much as can be derived. Alpine Shop is still in transition along with three other teams, but we don't know if anybody is already out on the next section. Ordinarily, I'd just ask, but I'm afraid that doing so would turn up the pressure on Yvonne who is moving well, but still clearly holding back. There's not really anything I'd do with that information, anyway. The way to win an adventure race is to get through the course as fast as you can. Thinking about what other teams are doing is a good way to make a silly and costly mistake.
At the transition we plot the points for the remainder of the course (which must be taken in order). With Yvonne calling out the coordinates and I plotting, we get done in eight minutes, which is reasonably speedy considering how long it's been since we've done this together. I can only assume that we then hit a rift in the time-space continuum, because a full ten minutes disappears while we are changing our shoes and getting our bikes out of the pit. We are definitely out of practice in transitions.
The first part of the bike is on roads and the first big descent reminds us that it hasn't warmed above freezing yet. We get to the spot where we are to leave the road, but we can't find the control anywhere. I try to find our coordinates sheet in my pack to see if the control clue has any additional information, but I can't find that either. After about five minutes of frantic searching another team comes along and confidently turns onto the trail. We decide to follow and get to the control after about a quarter mile. It's an annoying mistake, but not terribly costly. One of the nice things about racing with Yvonne is that this sort of thing doesn't rattle her at all. We push a bit and soon the other team is out of sight behind us.
The trail turns to singletrack on the Meramec flood plain. With everything frozen, it's pretty quick going. Not long after 10AM, we arrive at the next exchange. We are going to have to paddle with our bikes in the canoe because we'll need them for the final section in Castlewood. Fortunately, Yvonne's bike is so small, simply removing the front wheel is enough to fit the entire thing under the thwarts. We then wedge my rear wheel under a thwart and use our tow cable to secure the front. It's a decent exchange and we're underway in just a few minutes.
The first control is upstream and it's a fair current. After getting that, the rest of the paddle is downstream to the takeout at Castlewood beach. It's still around freezing, but the sky is clear and the sun has cleared the bluffs along the river, so the conditions are borderline pleasant. The whole thing takes about an hour and it has us wondering if there might be a surprise extra section waiting for us at the "finish". If not, this race isn't going to be anywhere near 8 hours.
The canoe to bike exchange takes longer than I'd like because we have to haul the boat a few hundred meters from the beach to the parking lot. Normally, this would be an easy portage with me carrying boat overhead while Yvonne ferried the rest of our gear. However, my shoulder certainly isn't going to stand for that (I'm still amazed it made it through the paddle without complaint), so we're stuck with lugging it with one of us on each end and then going back for all the rest of our stuff. Team Bushwacker passes us in the transition, but since they're another 4-person team, we're not too worried about it. It does occur to me that if we're still seeing nationally ranked teams at this late stage, we must be doing OK.
The final bike leg might hold some challenge for an out-of-town team, but for the locals, it's trivial. Castlewood is the most popular mountain biking venue in St. Louis and everybody has the trail network pretty much memorized. I even consider leaving the map in my pack but that seems a silly risk. Riding with the map clipped to the front of the pack isn't really any slower and it eliminates the chance of skipping a control due to late race brain fade. We zip through the course, noting that the ground is starting soften and later teams might have some mud to deal with. With a mile to go we catch Bushwacker; one of their members has broken a chain. I'm surprised they stopped to fix it, since it's almost all downhill to the finish. Seems like coasting/running it in would be a good deal quicker than getting out the tools. At any rate, we're happy to have the place back.
We get to the finish at 12:30 and Alpine Shop (having smoked the second half of the course to finish first) is there to greet us. We don't see too many other folks around, so we go ahead and finally ask where we stand. Fifth overall, first 2-person co-ed. Well, like I said at the start, I would have taken just about any result but a division win makes it a pretty sweet reunion. Yvonne is positively beaming and after a while I realize that I am, too. The hardest part of next season has already been taken care of. Carol's Team is back.
December 5, 2009
I've written before that the hardest part of Adventure Racing is putting the team together. I don't mean that as a joke, either. Adventure Racing is all about being reasonably good at a lot of things. Excellence is not required but, as David Frei likes to say, "You can't suck at anything." Almost anybody can learn this stuff, but it takes a LOT of time to learn it all. Finding others who are willing to spend the time (or better yet, have already spent the time) is really tough. So, when Yvonne Deyo agreed to team up for the Castlewood 8- Hour after a 5-year hiatus (during which she produced two children) that was cause for celebration regardless of the outcome.
But, expectations can be a tricky thing to manage. Yvonne's last Adventure Race was when she, David, and I took fourth at 2004 National Championships. At the time, she was widely regarded as one of the best female amateurs in the country. Her return has been the subject of continuous speculation and now that the day is at hand there are more than a few teams taking notice.
While she has done an excellent job of staying generally fit through two pregnancies, there's a big difference between being "in shape" and being ready for a race of this distance. Her situation is further compromised by the fact that she had recently injured her hamstring. While it held up the previous week at the St. Louis 3-hour orienteering meet (where she took the Women's title), she still has to be careful not to re-injure it.
So while we cheerfully tell each other that it is just great to be back racing together, the truth is we are both harboring a fair bit of pre-race anxiety. Her, because the crucible of competition often produces answers to questions you'd just as soon not have asked. And me because, let's be frank, my last outing (Berryman 36-hour in September) was an unmitigated disaster and, if I race like that here, she might just accept one of the dozens of standing offers to race on another team.
We are bused from Castlewood to the start at Greensfelder. It's a balmy 17F as we wait for the 7AM start. We're given our maps for the first section a few minutes before the start. We can take the first 11 controls in any order. Then there are a few more down to the bike exchange. Between nerves and the cold I'm shaking so badly I can hardly draw the lines to connect the control circles to indicate our route. Fortunately, the first thing we have to do is run a couple kilometers on road to where our punch cards are waiting. Even though we take it quite slow (no point in risking aggravating Yvonne's injury in the first 10 minutes of the race), it's enough that we both stop shivering.
We're pretty near the back of the field (and at 100 teams, it's a pretty big field for a regional race) when we leave the road to cut straight through the woods to the card pickup. Almost all the teams take the longer route on the road, but the road is so steep, the usual speed advantage isn't there. Plus, by climbing the steeper route, we can use the tow and make better progress up the hill. We end up being one of first teams into the pickup.
Now the real navigation starts. By orienteering standards, the controls would be considered a mix of intermediate and advanced. That puts them in the "Super Hard" category of Adventure Racing controls. Although the map we're using is old, it is a real orienteering map as opposed to the usual USGS quad. This all adds up to a big advantage for the teams like ours that have considerable orienteering experience.
Another such team is Alpine Shop. While we're technically not competing against them (they're in the 4-person division), as the #1 ranked team in the country, they provide a pretty good standard to measure by. They've all raced for Carol's Team at one point or another and we're all good friends, so when we meet them at the fifth control, I can't resist throwing a few taunts their way. Not to be outdone, they fire back just as quickly. Tempting as it is to lock horns with them in our favorite discipline, prudence dictates letting them go. Out game plan is "easy pace, no mistakes" and we have no idea what is in store for us after this initial section is done. Yvonne continues to use the tow on the climbs and we run at a steady, but conservative pace the rest of the time.
A couple controls later we get to one where the bag is hung from a tree growing out from a nearly vertical embankment. Getting to the control from above isn't particularly tough, but rather than slide down the embankment, I decide to climb back up. As I twist and grab another tree to swing back up to the top, my shoulder decides to pop out of the socket.
This isn't exactly a novel maneuver for my right shoulder. This is the third dislocation to match an equal number of separations. I let out enough of a yell that another team comes over to assist, but there really isn't much to be done. It appears our race is over. Then, as I move to get back up, it suddenly snaps back into the socket with an audible pop. Perhaps it's just in contrast to the pain that preceded, but it really feels OK. Yvonne looks for a cue and I just say, "Let's go."
We take it easy for a while since the footing on Greensfelder's steep ridges is spotty and a fall in this state could be disastrous. Still, the navigation is sufficiently technical that even at a slow pace, we're doing well by being accurate. Accurate enough, in fact, that we end up meeting Alpine Shop again. David is handling the maps as usual and he is despondent. This technical nav section was his chance to get them a clear lead but an error has set them back.
The optimal route through the controls seemed pretty obvious to me, and apparently David agreed as we are hitting them in the same order. However, there are certainly differences of opinion on that. At each control, teams are coming and going in all different directions, so it's very hard to know where we really stand. We hang with Alpine Shop for a couple legs, but they are clearly on a mission to get back in the lead and we have to let them go.
We arrive at the exchange area at 8:45. While it's obvious from the nearly 300 bikes lying around that we're doing well, that's as much as can be derived. Alpine Shop is still in transition along with three other teams, but we don't know if anybody is already out on the next section. Ordinarily, I'd just ask, but I'm afraid that doing so would turn up the pressure on Yvonne who is moving well, but still clearly holding back. There's not really anything I'd do with that information, anyway. The way to win an adventure race is to get through the course as fast as you can. Thinking about what other teams are doing is a good way to make a silly and costly mistake.
At the transition we plot the points for the remainder of the course (which must be taken in order). With Yvonne calling out the coordinates and I plotting, we get done in eight minutes, which is reasonably speedy considering how long it's been since we've done this together. I can only assume that we then hit a rift in the time-space continuum, because a full ten minutes disappears while we are changing our shoes and getting our bikes out of the pit. We are definitely out of practice in transitions.
The first part of the bike is on roads and the first big descent reminds us that it hasn't warmed above freezing yet. We get to the spot where we are to leave the road, but we can't find the control anywhere. I try to find our coordinates sheet in my pack to see if the control clue has any additional information, but I can't find that either. After about five minutes of frantic searching another team comes along and confidently turns onto the trail. We decide to follow and get to the control after about a quarter mile. It's an annoying mistake, but not terribly costly. One of the nice things about racing with Yvonne is that this sort of thing doesn't rattle her at all. We push a bit and soon the other team is out of sight behind us.
The trail turns to singletrack on the Meramec flood plain. With everything frozen, it's pretty quick going. Not long after 10AM, we arrive at the next exchange. We are going to have to paddle with our bikes in the canoe because we'll need them for the final section in Castlewood. Fortunately, Yvonne's bike is so small, simply removing the front wheel is enough to fit the entire thing under the thwarts. We then wedge my rear wheel under a thwart and use our tow cable to secure the front. It's a decent exchange and we're underway in just a few minutes.
The first control is upstream and it's a fair current. After getting that, the rest of the paddle is downstream to the takeout at Castlewood beach. It's still around freezing, but the sky is clear and the sun has cleared the bluffs along the river, so the conditions are borderline pleasant. The whole thing takes about an hour and it has us wondering if there might be a surprise extra section waiting for us at the "finish". If not, this race isn't going to be anywhere near 8 hours.
The canoe to bike exchange takes longer than I'd like because we have to haul the boat a few hundred meters from the beach to the parking lot. Normally, this would be an easy portage with me carrying boat overhead while Yvonne ferried the rest of our gear. However, my shoulder certainly isn't going to stand for that (I'm still amazed it made it through the paddle without complaint), so we're stuck with lugging it with one of us on each end and then going back for all the rest of our stuff. Team Bushwacker passes us in the transition, but since they're another 4-person team, we're not too worried about it. It does occur to me that if we're still seeing nationally ranked teams at this late stage, we must be doing OK.
The final bike leg might hold some challenge for an out-of-town team, but for the locals, it's trivial. Castlewood is the most popular mountain biking venue in St. Louis and everybody has the trail network pretty much memorized. I even consider leaving the map in my pack but that seems a silly risk. Riding with the map clipped to the front of the pack isn't really any slower and it eliminates the chance of skipping a control due to late race brain fade. We zip through the course, noting that the ground is starting soften and later teams might have some mud to deal with. With a mile to go we catch Bushwacker; one of their members has broken a chain. I'm surprised they stopped to fix it, since it's almost all downhill to the finish. Seems like coasting/running it in would be a good deal quicker than getting out the tools. At any rate, we're happy to have the place back.
We get to the finish at 12:30 and Alpine Shop (having smoked the second half of the course to finish first) is there to greet us. We don't see too many other folks around, so we go ahead and finally ask where we stand. Fifth overall, first 2-person co-ed. Well, like I said at the start, I would have taken just about any result but a division win makes it a pretty sweet reunion. Yvonne is positively beaming and after a while I realize that I am, too. The hardest part of next season has already been taken care of. Carol's Team is back.
Friday, December 2, 2016
Big Data
I (finally) got my data ingestion stuff done for CISS. That means I can pull a whole initiative data set from work and see how this thing runs. Other than getting those results, my adviser thinks I've done enough for the semester. Yay for that. I should be wrapped up next week and can enjoy our annual pilgrimage to Pere Marquette next weekend.
Thursday, December 1, 2016
Transcendental Functions
Back to Analysis for a few days...
The name comes from the fact that these functions transcend "normal" algebraic operations. That is, you can't express them as a finite set of additions, multiplications, roots, or their inverses. While there are an infinite number of such functions, several are of particular importance because they a) are solutions to ordinary differential equations and b) come up a lot in normal situations. (Devotees of classical physics would argue that (a) implies (b)). In fact, we're so familiar with them, it's easy to forget that they cannot be expressed in closed form. We can deal only in approximations.
Exponential:
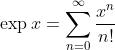
From our convergence results, it's fairly easy to show that (exp x)(exp y) = exp(x + y). It should also be fairly clear that exp 0 = 1 (since the first term, 00/0! = 1 is the only non-zero term in the sequence). It takes a bit more finagling to get that exp 1 = e, from which we finally can derive that exp x = ex.
The really important result is that d/dx exp x = exp x. That's why it pops up in the solution of so many differential equations.
Natural log: log x = exp-1x.
Since exp x is strictly increasing, we can invert it, though the domain is now just the positive real numbers (since exp x > 0). As with the exponential, the most useful result is related to it's derivative: d/dx log x = 1/x.
Trig functions: We all learned about these in high school as ratios of the sides of a right triangle: SOHCAHTOA (sin = opposite/hypotenuse, cos = adjacent/hypotenuse, tan = opposite/adjacent). While that's an easy way to remember them (even if a bit politically incorrect as kids of my generation were taught to say it like it was the name of an indian chief), the analytic versions are more interesting (at least, to me).
^n\frac{x^{2n+1}}{(2n+1)!}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+...\\&space;\cos&space;x=\sum_{n=0}^\infty(-1)^n\frac{x^{2n}}{(2n)!}=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+...\\)
The fact that those relate to either right triangles or the unit circle is less than obvious. The way you get there is a case study in incremental proof.
Start by noting that, when x = 0, both sequences are degenerate and sin 0 = 0, cos 0 = 1. It should also be obvious that negating x does nothing to cos, but it flips the sign of all the terms on sin. So, cos -x = cos x and sin -x = sin x. It is only slightly harder to take the derivatives and note that sin'x = cos x and cos'x = -sin x.
Armed with those facts, we can now show that g(x) = (sin x)2 + (cos x)2 = 1. Take the derivative:
g'(x) = 2(sin x)(cos x) + 2(cos x)(-sin x) = 0.
If the derivative is zero everywhere, then g(x) is constant. Thus,
g(x) = g(0) = 02 + 12 = 1.
Thus, (cos x, sin x) describe a point on the unit circle where x is the angle in radians and the normal trig identities fall into place. As a bonus, formulating the the trig functions as infinite alternating series allows us to derive arbitrarily precise bounds on estimates of such (you're never off by more than the first term you drop), as well as giving us a means for estimating π (though, unless you're grinding a telescope lense or launching a satellite, 22/7 will do just fine for the latter).
The name comes from the fact that these functions transcend "normal" algebraic operations. That is, you can't express them as a finite set of additions, multiplications, roots, or their inverses. While there are an infinite number of such functions, several are of particular importance because they a) are solutions to ordinary differential equations and b) come up a lot in normal situations. (Devotees of classical physics would argue that (a) implies (b)). In fact, we're so familiar with them, it's easy to forget that they cannot be expressed in closed form. We can deal only in approximations.
Exponential:
From our convergence results, it's fairly easy to show that (exp x)(exp y) = exp(x + y). It should also be fairly clear that exp 0 = 1 (since the first term, 00/0! = 1 is the only non-zero term in the sequence). It takes a bit more finagling to get that exp 1 = e, from which we finally can derive that exp x = ex.
The really important result is that d/dx exp x = exp x. That's why it pops up in the solution of so many differential equations.
Natural log: log x = exp-1x.
Since exp x is strictly increasing, we can invert it, though the domain is now just the positive real numbers (since exp x > 0). As with the exponential, the most useful result is related to it's derivative: d/dx log x = 1/x.
Trig functions: We all learned about these in high school as ratios of the sides of a right triangle: SOHCAHTOA (sin = opposite/hypotenuse, cos = adjacent/hypotenuse, tan = opposite/adjacent). While that's an easy way to remember them (even if a bit politically incorrect as kids of my generation were taught to say it like it was the name of an indian chief), the analytic versions are more interesting (at least, to me).
The fact that those relate to either right triangles or the unit circle is less than obvious. The way you get there is a case study in incremental proof.
Start by noting that, when x = 0, both sequences are degenerate and sin 0 = 0, cos 0 = 1. It should also be obvious that negating x does nothing to cos, but it flips the sign of all the terms on sin. So, cos -x = cos x and sin -x = sin x. It is only slightly harder to take the derivatives and note that sin'x = cos x and cos'x = -sin x.
Armed with those facts, we can now show that g(x) = (sin x)2 + (cos x)2 = 1. Take the derivative:
g'(x) = 2(sin x)(cos x) + 2(cos x)(-sin x) = 0.
If the derivative is zero everywhere, then g(x) is constant. Thus,
g(x) = g(0) = 02 + 12 = 1.
Thus, (cos x, sin x) describe a point on the unit circle where x is the angle in radians and the normal trig identities fall into place. As a bonus, formulating the the trig functions as infinite alternating series allows us to derive arbitrarily precise bounds on estimates of such (you're never off by more than the first term you drop), as well as giving us a means for estimating π (though, unless you're grinding a telescope lense or launching a satellite, 22/7 will do just fine for the latter).
Wednesday, November 30, 2016
Link functions
Sometimes I forget just how new statistics is. Informal measurement and inference predate history. Measure theory, which laid the mathematical foundations for random variables and distributions came about in response to the formalization of Calculus in the 17th century. But, actual mathematically-based statistics? That really didn't get going until the work of Fisher. He died the year before I was born. On the timeline of human knowledge, this is really new stuff.
I mention that because I attended a colloquium today on Dimension Reduction by Dr. Wen of MS&T (the engineering school formerly known as Rolla) and she threw out the term "Link Function". It wasn't the first time I'd heard it; I knew it had something to do with tying the mean to the predictors in a Generalized Linear Model (GLM), but I decided that I'd better file it under the heading of "Named Results" and actually learn what it was.
Turns out, there's a very good reason I didn't know what it was: the term didn't get widespread use until after I got my MS. I checked my text from Cornell (the rightly acclaimed Mathematical Statistics by Bickel and Docksum) and they mention the function in the context of the General Linear Model, but it's just given the anonymous designation g. The "generalization" of the linear model into the Generalized Linear Model was published in 1972, but it didn't really catch on until after B&D's publication in 1977, when computing power became cheap enough that anybody could afford to run their data through a package like GLIM. The function is still generally written as g, but it has also picked up the moniker of the Link Function.
So, what is the link function? It's actually rather well named - it provides a "link" from the mean to the linear predictor. So, if μi is the mean of our observed dependent variable, the link function g(μi) then maps that to the real number line and calls that the linear predictor. The linear predictor is modeled as a linear combination of the independent variables plus an error term which follows a normal distribution. It's sort of like a transformation, but not quite. With a transformation, you transform both the predictor and the error term. Here, the link function is only transforming the predictor.
I mention that because I attended a colloquium today on Dimension Reduction by Dr. Wen of MS&T (the engineering school formerly known as Rolla) and she threw out the term "Link Function". It wasn't the first time I'd heard it; I knew it had something to do with tying the mean to the predictors in a Generalized Linear Model (GLM), but I decided that I'd better file it under the heading of "Named Results" and actually learn what it was.
Turns out, there's a very good reason I didn't know what it was: the term didn't get widespread use until after I got my MS. I checked my text from Cornell (the rightly acclaimed Mathematical Statistics by Bickel and Docksum) and they mention the function in the context of the General Linear Model, but it's just given the anonymous designation g. The "generalization" of the linear model into the Generalized Linear Model was published in 1972, but it didn't really catch on until after B&D's publication in 1977, when computing power became cheap enough that anybody could afford to run their data through a package like GLIM. The function is still generally written as g, but it has also picked up the moniker of the Link Function.
So, what is the link function? It's actually rather well named - it provides a "link" from the mean to the linear predictor. So, if μi is the mean of our observed dependent variable, the link function g(μi) then maps that to the real number line and calls that the linear predictor. The linear predictor is modeled as a linear combination of the independent variables plus an error term which follows a normal distribution. It's sort of like a transformation, but not quite. With a transformation, you transform both the predictor and the error term. Here, the link function is only transforming the predictor.
Tuesday, November 29, 2016
Box-Muller random normal generation
This topic might be considered a bit archaic since any decent stats package comes with functions that will generate random numbers from any of the major distributions. That said, somebody has to actually write those routines and knowing how its done is helpful for knowing the limitations. More to the point in my case: it might come up on the test.
We start with the assumption that we can generate a reasonably random sequence of U(0,1) random variables. This is, of course, a whole field of research in and of itself. However, for now, we'll just assume that we can do that. There are several ways to proceed from there.
If you want uniform random variables, well, you're pretty much done. Just scale and shift it to the interval you want.
When the pdf is closed form and invertible, plugging the uniform random variable (U) into the the inverse gets the job done. So, for example, if you want exponential random variables, just invert the exponential pdf, Y = FY-1(U) = -λ log(1-U) and you're done.
Of course a lot of distributions don't have nice, closed-form, invertible pdf's. In that case, you may be able to use a transform of one that does. "May" being the operative word. Some transforms are simpler than others.
Of particular note is the normal distribution. Since it comes up so frequently, one would obviously want to handle this case. However the normal pdf is not in closed-form and there's no good transformation from a variable that is. In an odd and fortuitous quick, there is a transformation from two random variables, one uniform, one exponential (the exponential, as shown above, would also likely come from a uniform). This method goes by both the Box-Muller algorithm (for it's creators) or the Polar method (which describes how you actually pull it off).
Without going into the formal proof, here's how it works. Start with the observations that, if Y ~ exp(1/2), then Y ~ χ22 and if X ~ N(0,1), then X2 ~ χ12. Therefore, the sum of two squared standard normals is exponential. There's not much one can immediately do with that, but it should at least suggest a relationship. In particular, what if we were to consider the normals as the legs of a right triangle and the exponential the hypotenuse? How many ways are there for that to happen? Well, you basically have the whole unit circle times the exponential length. So, let's randomly generate polar coordinates as uniform and exponential and then take the cartesian coordinates as normal.
Crunching the actual proof is not as daunting as it may seem. Once you see that switching to polar coordinates is your answer, it falls out pretty quickly. So, (without proof), if we have two uniform(0,1) random variables U1, U2 and R = (-2 log U1)1/2 and θ = 2πU2, then X1 = Rcosθ and X2 = Rsinθ are independent N(0,1) random variables.
Why stress over generating one when you can get two for cheap?
We start with the assumption that we can generate a reasonably random sequence of U(0,1) random variables. This is, of course, a whole field of research in and of itself. However, for now, we'll just assume that we can do that. There are several ways to proceed from there.
If you want uniform random variables, well, you're pretty much done. Just scale and shift it to the interval you want.
When the pdf is closed form and invertible, plugging the uniform random variable (U) into the the inverse gets the job done. So, for example, if you want exponential random variables, just invert the exponential pdf, Y = FY-1(U) = -λ log(1-U) and you're done.
Of course a lot of distributions don't have nice, closed-form, invertible pdf's. In that case, you may be able to use a transform of one that does. "May" being the operative word. Some transforms are simpler than others.
Of particular note is the normal distribution. Since it comes up so frequently, one would obviously want to handle this case. However the normal pdf is not in closed-form and there's no good transformation from a variable that is. In an odd and fortuitous quick, there is a transformation from two random variables, one uniform, one exponential (the exponential, as shown above, would also likely come from a uniform). This method goes by both the Box-Muller algorithm (for it's creators) or the Polar method (which describes how you actually pull it off).
Without going into the formal proof, here's how it works. Start with the observations that, if Y ~ exp(1/2), then Y ~ χ22 and if X ~ N(0,1), then X2 ~ χ12. Therefore, the sum of two squared standard normals is exponential. There's not much one can immediately do with that, but it should at least suggest a relationship. In particular, what if we were to consider the normals as the legs of a right triangle and the exponential the hypotenuse? How many ways are there for that to happen? Well, you basically have the whole unit circle times the exponential length. So, let's randomly generate polar coordinates as uniform and exponential and then take the cartesian coordinates as normal.
Crunching the actual proof is not as daunting as it may seem. Once you see that switching to polar coordinates is your answer, it falls out pretty quickly. So, (without proof), if we have two uniform(0,1) random variables U1, U2 and R = (-2 log U1)1/2 and θ = 2πU2, then X1 = Rcosθ and X2 = Rsinθ are independent N(0,1) random variables.
Why stress over generating one when you can get two for cheap?
Monday, November 28, 2016
More deltas
Before getting down to business, here's today's weird coincidence. For the CISS algorithm, I was deriving the point at which I should jump from the conservative uniform distribution on blocksums to the more aggressive exponential model. I decided to model the decision as a Null Hypothesis test, with a p-value of 5% (meaning you'd mistakenly switch to the exponential 1 in 20 times that you shouldn't). Due to the quirks of the inverse gamma distribution on the exponential prior, the first point at which this decision can be made is when three blocks have been sampled. So, how far away from the null mean does the observed mean need to be? The pdf of the Bates distribution is a big mess, but it simplifies if you are only looking at the lower tail:
&space;=&space;27x^2)
assuming three iid U(0,1) observations and x < 1/3. (Obviously, that gets scaled to reflect the upper bound being the maximum possible block sum for a stratum, but it's easier to compute the critical value first and then scale it). Thus, the cdf is:
=\int_{0}^{a}f_{\bar{X}}(x)dx=\frac{9a^3}{2})
OK, nothing interesting so far, but here's the weird part: set that equal to 0.05 and solve for a. You get 2/9. Really!
![\frac{2}{9}=\sqrt[3]{(0.05)\frac{2}{9}}](http://latex.codecogs.com/gif.latex?\frac{2}{9}=\sqrt[3]{(0.05)\frac{2}{9}})
There's no significance to the 2/9, the p-value is arbitrary, and it's an approximation (to 3 decimal places) not a real equality. It just turns out that 1/20 is roughly 2/9 squared. Still, it kinda leaps off the page at you.
OK, enough of that nonsense. Let's continue looking at the delta method. In the first-order case, the problem was that when g'(θ) = 0, there's no way to extrapolate a distribution because the approximating line is flat. The obvious step is to go to the second-order polynomial and hope for some variation there. So,
=g(\theta)+g'(\theta)(Y_n-\theta)+\frac{g''(\theta)}{2}(Y_n-\theta)^2+\textrm{Remainder})
which implies that
-g(\theta)=\frac{g''(\theta)}{2}(Y_n-\theta)^2+\textrm{Remainder})
since g'(θ) is zero. Since the square of a standard normal is chi-squared with 1 degree of freedom, we see that
![\frac{\sqrt{n}(Y_n-\theta)}{\sigma}\rightarrow N(0,1)~\textrm{in distribution}\\ \\ \Rightarrow\frac{n(Y_n-\theta)^2}{\sigma^2}\rightarrow \chi_1^2~\textrm{in distribution}\\ \\ \Rightarrow \frac{n[g(Y_n)-g(\theta)]}{\sigma^2}\rightarrow \frac{g''(\theta)}{2}\chi_1^2~\textrm{in distribution}\\](https://latex.codecogs.com/gif.latex?\frac{\sqrt{n}(Y_n-\theta)}{\sigma}\rightarrow&space;N(0,1)~\textrm{in&space;distribution}\\&space;\\&space;\Rightarrow\frac{n(Y_n-\theta)^2}{\sigma^2}\rightarrow&space;\chi_1^2~\textrm{in&space;distribution}\\&space;\\&space;\Rightarrow&space;\frac{n[g(Y_n)-g(\theta)]}{\sigma^2}\rightarrow&space;\frac{g''(\theta)}{2}\chi_1^2~\textrm{in&space;distribution}\\)
Of course, one does well to confirm the second derivative exists and is also not zero. Finally, since Taylor series work just fine in multidimensional space, it should be no surprise that there's a multivariate form of this method as well:
Let X1, ..., Xn be a random sample of p-dimensional vectors with E(Xij) = μi and Cov(Xik, Xjk) = σij. For a given function g with continuous first partial derivatives and a specific value of μ = (μ1, ..., μp) for which
![\tau^2=\sum\sum\sigma_{ij}\frac{\partial g(\mu)}{\partial \mu_i}\frac{\partial g(\mu)}{\partial \mu_j}>0,\\ \\ \sqrt{n}[g(\mathbf{\bar{X}})-g(\mathbf{\mu})]\rightarrow N(0,\tau^2)~\textrm{in distribution.}](https://latex.codecogs.com/gif.latex?\tau^2=\sum\sum\sigma_{ij}\frac{\partial&space;g(\mu)}{\partial&space;\mu_i}\frac{\partial&space;g(\mu)}{\partial&space;\mu_j}>0,\\&space;\\&space;\sqrt{n}[g(\mathbf{\bar{X}})-g(\mathbf{\mu})]\rightarrow&space;N(0,\tau^2)~\textrm{in&space;distribution.})
You can pull the second-order trick on this one, too, if you need to, but that rarely happens since all the partials would have to be zero to make the method fail.
assuming three iid U(0,1) observations and x < 1/3. (Obviously, that gets scaled to reflect the upper bound being the maximum possible block sum for a stratum, but it's easier to compute the critical value first and then scale it). Thus, the cdf is:
OK, nothing interesting so far, but here's the weird part: set that equal to 0.05 and solve for a. You get 2/9. Really!
There's no significance to the 2/9, the p-value is arbitrary, and it's an approximation (to 3 decimal places) not a real equality. It just turns out that 1/20 is roughly 2/9 squared. Still, it kinda leaps off the page at you.
OK, enough of that nonsense. Let's continue looking at the delta method. In the first-order case, the problem was that when g'(θ) = 0, there's no way to extrapolate a distribution because the approximating line is flat. The obvious step is to go to the second-order polynomial and hope for some variation there. So,
which implies that
since g'(θ) is zero. Since the square of a standard normal is chi-squared with 1 degree of freedom, we see that
Of course, one does well to confirm the second derivative exists and is also not zero. Finally, since Taylor series work just fine in multidimensional space, it should be no surprise that there's a multivariate form of this method as well:
Let X1, ..., Xn be a random sample of p-dimensional vectors with E(Xij) = μi and Cov(Xik, Xjk) = σij. For a given function g with continuous first partial derivatives and a specific value of μ = (μ1, ..., μp) for which
You can pull the second-order trick on this one, too, if you need to, but that rarely happens since all the partials would have to be zero to make the method fail.
Sunday, November 27, 2016
SLOC 3-Hour
The St. Louis Orienteering Club has been running a 3-hour score event the Saturday after Thanksgiving since, well, since long before I ran my first one in 1997. At least the last 40 years. Probably closer to 50. While it's a local meet, it typically attracts some serious out-of-town talent. The first time I won it (1998), I remember feeling like I had just won a national championship.
In recent years, the event has changed a bit; catering to the Adventure Racer side of the club. It's not easy to articulate the difference between AR "Trekking" and true "Orienteering", but anybody with more than superficial experience in both understands the distinction. It's not that one is harder or more worthy than the other, it's more a matter of structure. Orienteering has very specific rules regarding technical correctness. Adventure Racing, you take what comes. If you approach the latter with the mindset of the former, you will NOT enjoy the event. If you take a chill pill first, it's all good.
This year's version starts and finishes at Raging Rivers. It's a lidar-trail map in Illinois, upriver from Alton. By lidar-trail, I'm referring to the genre of maps which grab publicly available lidar elevation data, add trails and other super-obvious features, and call that good enough. While such mapping shortcuts throw the orienteering crowd into apoplectic fits, they are actually quite sufficient for navigation. What they are not good enough for is making good route choices, since vegetation density is not indicated. Fortunately, I've run these nasty, overgrown woods before and know that ANY trail route is better than ANY woods route.
The field is a bit lean this year. The nice weather has all the locals out, but there's only one big entry from out of town: Andrei Karpoff, who is going as a team with local Scott Erlandson (who goes by Erl). These two are the real deal, especially on an adventure-race-type map. Erl recently took home bronze in US Adventure Race National Championships (teamed with Emily Korsch, who is running solo today, and Justin Bakken). Andrei is also an excellent adventure racer and has handed me a defeat in some longer orienteering events, such as the Possum Trot. So, this will be no cakewalk.
The format is a mark-on-the-clock three hour score-O. At the gun, I run a firm pace over to the map boards so I have the luxury of sitting down with a map right in front of me rather than having to mark peering over someone else's shoulder. Past experience has shown that this is a bad time to rush. I take my time, making sure all the circles are in the right spot before heading out.
Controls 1-9 are 10 points each, 10-18 are 20, 20-24 are 30. For reasons not given, there's no control 19. While I expect to sweep the course, I follow the herd heading east from the start to make sure I get all the high-point controls. Many go straight up the ridge to 8. I decide to hit 4 and 7 first so I'll have a straight shot back to 6 on the return.
At 7, I get to the control location, which is pretty open by the standards of these woods, but still can't see the control anywhere. I'm almost to the point of giving up on it when I spot it lying on the ground in the reentrant. Orienteering: protest, course gets thrown out. Adventure racing: I put it on top of the log it was hung from so others will be able to see it.
At 7, I get to the control location, which is pretty open by the standards of these woods, but still can't see the control anywhere. I'm almost to the point of giving up on it when I spot it lying on the ground in the reentrant. Orienteering: protest, course gets thrown out. Adventure racing: I put it on top of the log it was hung from so others will be able to see it.
I pass Erl and Andrei on the way to 12. We meet up again at 13 and stay together through the long, very slow descent off the ridge. The woods are crazy thick here and I'm glad I'm with them or I'd be stressing over how much time I was losing. Since I'm keeping up with two of the best bushwackers in the country, I conclude that the woods are just crazy thick and there's nothing wrong with my pace.
The eastern loop is fun with its mix of, well, I can't call it "urban" but let's go with "small town" navigation and woods. Erl and Andrei skip 15, so they get a bit ahead of me. Emily, who has skipped 7, is also slightly up the road. We blast through 17, 16, 18, and 22, then start taking navigation a bit more seriously. The rockface between 23 and 24 is crossable, but not without risk. I take it cautiously and am starting to lose contact with the lead three who are apparently still young enough to believe they are impervious to injury.
I push to 21, missing the trail in the process. Apparently, my route through the woods isn't much worse because, once I do get on the trail, Emily is right in front of me. We hit 21 together. Leaving 21, I comment to her that there's no good attackpoint for 20. She agrees.
As I have no confidence in my attack from the top of the ridge, I figure I'll just take my best guess at which of the many spurs to descend and sort it out at the bottom if I'm wrong. At the bottom, it's obvious from the other reentrants coming together that I had actually descended the correct spur, but the control was not there. Emily is still with me. We look to the north where the visibility is better and see no control, so we start hunting south. Two spurs later, I'm starting to think that there's no way it could be off this much. I'm within seconds of turning around to head north when I spot the flag two more spurs over (the arrow on the map indicates the actual location). Another common ethos in Adventure Racing is that when a control is misplaced, competitors become allies and work together finding it. I call out that I've got it, but that turns out to be unnecessary. Emily has also spotted it, as have Andrei and Erl, who had been searching further up the hill. We all converge on the bag at about the same time.
I push to 21, missing the trail in the process. Apparently, my route through the woods isn't much worse because, once I do get on the trail, Emily is right in front of me. We hit 21 together. Leaving 21, I comment to her that there's no good attackpoint for 20. She agrees.
As I have no confidence in my attack from the top of the ridge, I figure I'll just take my best guess at which of the many spurs to descend and sort it out at the bottom if I'm wrong. At the bottom, it's obvious from the other reentrants coming together that I had actually descended the correct spur, but the control was not there. Emily is still with me. We look to the north where the visibility is better and see no control, so we start hunting south. Two spurs later, I'm starting to think that there's no way it could be off this much. I'm within seconds of turning around to head north when I spot the flag two more spurs over (the arrow on the map indicates the actual location). Another common ethos in Adventure Racing is that when a control is misplaced, competitors become allies and work together finding it. I call out that I've got it, but that turns out to be unnecessary. Emily has also spotted it, as have Andrei and Erl, who had been searching further up the hill. We all converge on the bag at about the same time.
The other three stay low, but I decide to get to the trail as quickly as possible to get out of the thick woods. This doesn't save any time as the woods get thicker near the top of the ridge. The last 20 meters to the trail are literally crawling on hands and knees. Once on the trail, it's very quick running down to 14. Erl and Andrei are about 30 seconds ahead heading south to get 15 and setting up a return on the road along the river. Emily is not in sight so I assume she's behind me. I head north for the long trail run to 6. The split has been made and the win will come down to executing these last few controls solo.
As I climb the ridge, my legs are reminding me that I ran 100 miles just two weeks ago. Still, they respond to prodding and, once on top of the ridge, I make great time to 6. Running the trail out of 6, I get in my obligatory fall as I get tripped up trying to jump over some storm debris. I go down pretty hard, but only my hand sustains an injury (and a minor one at that). I take a conservative route to 5 and hit it cleanly.
Leaving 5, I notice that the tail I was intending to take to 10 is actually marked as out of bounds. That's not a particularly pleasant revelation as it means I need to traverse the 500 meters over to 10. As this is the last stretch of thick woods I have to deal with, I'm able to stay focused and make pretty good time though it probably would have been faster to go back through 2 and run the field. At 10, I meet Erl and Andrei again, coming the other way. They head downhill towards 3. If they only have 3, 2, and 5 to go, this is going to be very, very close.
I'm too tired to push through thick woods and any navigation error now would be disastrous. Fortunately, the trail routes are fast, simple, and not much extra distance so I can run them full speed and still hit 11 and 3 cleanly. Heading towards 2, I pass Emily who's on her way up to 3. Erl and Andrei will have to cross in front of me to get to the finish. I don't see them pass and I can't believe they are more than a minute or two ahead of me, so it looks like I'm leading. Problem is, I squander a few seconds locating 2 and, once I've found it, I have to crawl through some vegetation to get to it. I'm in a complete panic as I crawl back out; having them come by at this point would be too much to bear. I emerge from the woods and see nobody in front, so I hit the gas for the line.
Turns out, they hadn't got 6 yet, so I actually beat them by a few minutes to take the overall win in two hours, four minutes (somebody probably wrote seconds down somewhere but, again, this is Adventure Racing and we don't need to concern ourselves with digits that don't matter). Emily comes in a few minutes after them to take the women's prize. The course setter, Jerry Young, apologizes that the course was a bit short. I respond that my legs were more than happy to stop.
The misplaced control and the unmapped thick woods would have ruined a "true" orienteering event. However, this race was just a whole lot of fun. I went into it with a relaxed attitude and really enjoyed not only the fast sections, but dealing with the vegetation as it came. In truth, I think Jerry did a pretty good job of keeping us out of the worst of it. And, oscillating between pushing through the woods and blasting the trails was pretty much the only way I could have run competitively on just two weeks recovery from Tunnel Hill. On a more open course (or one closer to the full three hours), I would simply not have been able to maintain a decent pace.
The event has definitely changed over the past 20 years, but not for the worse. Local turnout was excellent and the mood at the finish was buoyant. Veterans and newbies alike returned with smiles. There was a time, not long ago, when I would have decried the fact that having fun was taking precedence over rigorous competition. I'm pretty much over that one.
The event has definitely changed over the past 20 years, but not for the worse. Local turnout was excellent and the mood at the finish was buoyant. Veterans and newbies alike returned with smiles. There was a time, not long ago, when I would have decried the fact that having fun was taking precedence over rigorous competition. I'm pretty much over that one.
Subscribe to:
Posts (Atom)





