Usually named results are named after somebody. Then there's the unfortunate result that is given such a catchy name that nobody remembers who came up with it. The squeeze theorem is one such result:
Let {an}, {bn}, {cn} be sequences such that an ≤ bn ≤ cn. If {an} and {cn} converge to the same limit, L, then {bn} converges to L.
As with many analysis results, it seems pretty obvious. But, it's also really, really useful. Enough so, that if I was the one who came up with this, I'd be pissed it wasn't called Buckley's Theorem. So, I've decided that my thesis topic, which is basically an optimal stopping rule for sampling large databases will be called the Targeted Incremental Transform Search and Assessment. That way, if it doesn't get named Buckley's Algorithm, it will at least get called TITS and Ass. I'd be fine with that.
Friday, September 30, 2016
Thursday, September 29, 2016
Well-ordered
No we're not talking restaurant etiquette, this named result is about the positive integers. It states simply that if X is a non-empty set of positive integers, there is a "least" element of X, that is a value that is less than or equal to every other element in the set.
Seems obvious enough. Depending on how many intermediate results you're willing to establish prior to proving the actual theorem, the proof is pretty straightforward as well. Next question is: why does anybody care?
Well, as with the whole least upper bound thing, it comes in handy in a variety of situations to know that you can actually produce a minimum from any set of positive integers (and, by corollaries, mins and maxes of any bounded set of integers). It's not the sort of thing that you want to have to argue in the middle of a complex proof. So, you name it and get on with life.
A related result is also named: the positive integers are Archimedean Ordered, that is, for every two positive integers, a, b, there is some n such that a < bn. Not exactly sure why that matters, but the immediate corollary is useful when taking limits: for any real number ε > 0, there exists a positive integer n such that 1/n < ε.
And you should never order your steak well. Medium-rare at most.
Seems obvious enough. Depending on how many intermediate results you're willing to establish prior to proving the actual theorem, the proof is pretty straightforward as well. Next question is: why does anybody care?
Well, as with the whole least upper bound thing, it comes in handy in a variety of situations to know that you can actually produce a minimum from any set of positive integers (and, by corollaries, mins and maxes of any bounded set of integers). It's not the sort of thing that you want to have to argue in the middle of a complex proof. So, you name it and get on with life.
A related result is also named: the positive integers are Archimedean Ordered, that is, for every two positive integers, a, b, there is some n such that a < bn. Not exactly sure why that matters, but the immediate corollary is useful when taking limits: for any real number ε > 0, there exists a positive integer n such that 1/n < ε.
And you should never order your steak well. Medium-rare at most.
Wednesday, September 28, 2016
The real axioms
I'm pivoting over to Analysis for a bit in my quest for named results. We'll start at the beginning: the axioms of the real number line. These aren't, technically, named results because they aren't proven. They are, well, axiomatic. A set R of numbers is the set of real numbers if it meets the following conditions:
- R is closed under addition. (Never mind what "addition" is just yet; other than a binary operator represented by "+").
- Addition is associative in R, that is, (x + y) + z = x + (y + z).
- Addition is commutative in R, that is x + y = y + x.
- An additive identity element exists in R, denoted "0", such that x + 0 = x.
- All elements of R have an additive inverse. That is, for all x there exists y such that x + y = 0. (We denote such an inverse of x as -x).
These five axioms define a commutative (or abelian) group. There are lots of such groups, we need more.
- R is closed under multiplication. (Again, don't worry about what that is, other than we'll denote it by "*" or, if we're really feeling hip, we'll leave out the operator altogether so only our close friends are in on the joke.
- Multiplication is associative.
- Multiplication is commutative.
- A multiplicative identity exists, denoted "1".
- All non-zero elements of R have a multiplicative inverse, that is xy = 1. (We denote such an inverse as x-1 or 1/x).
So, couldn't you just make 0 = 1 and let addition and multiplication be the same thing? Yup, you sure could, until we hit you with the next axiom:
- Multiplication distributes over addition. That is: x(y + z) = xy + xz and (x + y)z = xz + yz. This leads to three trivial results that are nonetheless important: 1) 1 ≠ 0, 2) + ≠ *, and 3) 0 * x = 0.
Sets meeting these eleven axioms are called a field. There are lots of fields as well.
- There is a subset P of R (called the positive numbers) that is closed under addition such that, for all x in R, exactly one of the following statements is true:
- x∈P
- x = 0
- -x∈P
While it's not super obvious, this is the axiom that gives us the ability to order numbers, essentially by putting x - y into one of the three groups to get x > y, x = y, and x < y, respectively. It also allows proving the transitive property of ordering and that 1 > 0.
Almost home, but the rationals also meet the above 12 axioms. We need one more to uniquely define the reals: completeness.
- A nonempty subset of R which is bounded above has a least upper bound.
Really? Seems like a nutty axiom, but it's not. It basically means that there are no "holes" in the real line. If the completeness axiom was not true, you would have open subsets where you couldn't add the endpoint to close them, because the endpoint wasn't part of the set. For example, consider the set of rationals less than π. This is an open set that can't be closed because π isn't in the set of rationals. You can come up with increasingly better bounds, but any rational bound you chose would give you a different set.
So, that's it. The dirty baker's dozen defining the real numbers. Any set satisfying these axioms is isomorphic to the reals, that is, it's the same set labeled differently.
So, that's it. The dirty baker's dozen defining the real numbers. Any set satisfying these axioms is isomorphic to the reals, that is, it's the same set labeled differently.
Tuesday, September 27, 2016
Transform of a discrete random variable by it's CDF
I'm only posting on this one because I ended up spending an inordinate amount of time on it. It's a problem from one of the texts I'm using. The authors suggest an argument based on a picture of the cdf which is obvious enough. However, much of the mess of mathematics in the 18th and 19th centuries was a result of the fact that people were too quick to resort to "proof by picture" rather than strict rules of logic. (Of course, the mess since then is an even bigger one stemming from the fact that the strict rules of logic don't really work that well, either; but that's another day's discussion).
Anyway, as grad-level probability theory is in pretty safe turf from an existential argument point of view, I decided to work out a more formal proof. The result in question is the discrete version of the well-known transformation that F(X) ~ U(0,1). That is, if you feed a continuous random variable back into its own cdf, you get a standard uniform random variable. In the discrete case, it's not quite so pretty. Instead the best you can say is that you get a random variable that is bounded by [0,1] and is stochastically greater than U(0,1).
A clue as to where to start is the proof in the continuous case, which is pretty straightforward:
Let Y = FX(X).
Then
FY(y) = P(Y ≤ y)
= P(FX(X) ≤ y)
= P(FX-1[FX(X)] < FX-1(y))
= P(X ≤ FX-1(y))
= FX(FX-1(y))
= y
Which implies Y ~ U(0,1).
Here, FX-1(y) is well defined even if the cdf is not strictly increasing by setting
FX-1(y) = inf {x| FX(x) = y}
Now, we have to look at why the equality doesn't hold for discrete random variables. The answer is that the inverse function is no longer well defined. It may well be that no value of x satisfies FX(x) = y. Therefore, we need to add an inequality:
FX-1(y) = inf {x| FX(x) ≥ y}
It's fairly easy to show that, on points where P(X = x) > 0, the equality still holds. Therefore, we still have P(FX-1[FX(X)] < FX-1(y)) = P(X ≤ FX-1(y)) = FX(FX-1(y)). It's the final line where things break down. Here, we can't count on y being in the set of {FX(x) | P(X = x) > 0}, so the inequality comes into play. Specifically, when P(X = FX-1(y)) = 0, we get FX(FX-1(y)) < y. As X is discrete, there are infinitely many points where P(X = FX-1(y)) = 0 and we only need one to establish that Y is stochastically greater than U(0,1).
Anyway, as grad-level probability theory is in pretty safe turf from an existential argument point of view, I decided to work out a more formal proof. The result in question is the discrete version of the well-known transformation that F(X) ~ U(0,1). That is, if you feed a continuous random variable back into its own cdf, you get a standard uniform random variable. In the discrete case, it's not quite so pretty. Instead the best you can say is that you get a random variable that is bounded by [0,1] and is stochastically greater than U(0,1).
A clue as to where to start is the proof in the continuous case, which is pretty straightforward:
Let Y = FX(X).
Then
FY(y) = P(Y ≤ y)
= P(FX(X) ≤ y)
= P(FX-1[FX(X)] < FX-1(y))
= P(X ≤ FX-1(y))
= FX(FX-1(y))
= y
Which implies Y ~ U(0,1).
Here, FX-1(y) is well defined even if the cdf is not strictly increasing by setting
FX-1(y) = inf {x| FX(x) = y}
Now, we have to look at why the equality doesn't hold for discrete random variables. The answer is that the inverse function is no longer well defined. It may well be that no value of x satisfies FX(x) = y. Therefore, we need to add an inequality:
FX-1(y) = inf {x| FX(x) ≥ y}
It's fairly easy to show that, on points where P(X = x) > 0, the equality still holds. Therefore, we still have P(FX-1[FX(X)] < FX-1(y)) = P(X ≤ FX-1(y)) = FX(FX-1(y)). It's the final line where things break down. Here, we can't count on y being in the set of {FX(x) | P(X = x) > 0}, so the inequality comes into play. Specifically, when P(X = FX-1(y)) = 0, we get FX(FX-1(y)) < y. As X is discrete, there are infinitely many points where P(X = FX-1(y)) = 0 and we only need one to establish that Y is stochastically greater than U(0,1).
Monday, September 26, 2016
The best way to learn
Looking at my study log, it appears I've only put in around 8 hours a week for the past few weeks. That's certainly not going to get the job done; time to step it up a bit.
Meanwhile, an explanation of the posts of late is in order. I did fine in undergrad (well, the first year was a bit of a mess, but working on a farm the following summer provided sufficient motivation to fix that). While the graduate coursework at Cornell was significantly more challenging (no surprise there), I still did a fair job of getting through it. In short, by the time I had my masters, I felt I had done a pretty good job of learning stuff.
And, I suppose I had, but there is a whole 'nuther level beyond getting A's.
Once I started teaching, I realized that I could answer any question covered by the courses I had taught. Any. As in, I would get 100% on any reasonable test of the material. "The best way to learn something is to teach it" may be a cliche, but it's also true.
The reason, I believe, is twofold. First and foremost, there is a huge incentive to show up to class knowing the material: you look like an idiot if you don't. The students are supposed to struggle; the prof is not. Secondly, when the questions do come, they force you to rethink your presentation. Simply repeating what you just said won't help someone who didn't get it the first time. You need to find a different way to communicate the idea. This not only reinforces the idea; but also opens your mind to connections between ideas that might not have been apparent under the original presentation. The more connected the knowledge, the easier it is to retain it.
The confluence of these is that, when preparing for a lecture, good professors will anticipate the areas where students stumble and think about alternate ways to present it. My strategy was generally to make my first explanation different than what was in the text. That way, if students had already read the text (no, I'm not naive enough to think that most students read the text before the lecture), they would already be on the second explanation. If not, and a question came up, I could always fall back on what was in the text. This meant that I had dual explanations for pretty much everything the course covered. That's a powerful set of knowledge.
So that's what I'm trying to do with these named results. I come across the result in the text, and I try to figure out how I would present it differently to a class being taught out of this text. Sure, it would be even better to actually teach the class, but I think this method is pretty effective. Of course, there's no substitute for practice, so I really do need to up the hours and work more problems as well.
Meanwhile, an explanation of the posts of late is in order. I did fine in undergrad (well, the first year was a bit of a mess, but working on a farm the following summer provided sufficient motivation to fix that). While the graduate coursework at Cornell was significantly more challenging (no surprise there), I still did a fair job of getting through it. In short, by the time I had my masters, I felt I had done a pretty good job of learning stuff.
And, I suppose I had, but there is a whole 'nuther level beyond getting A's.
Once I started teaching, I realized that I could answer any question covered by the courses I had taught. Any. As in, I would get 100% on any reasonable test of the material. "The best way to learn something is to teach it" may be a cliche, but it's also true.
The reason, I believe, is twofold. First and foremost, there is a huge incentive to show up to class knowing the material: you look like an idiot if you don't. The students are supposed to struggle; the prof is not. Secondly, when the questions do come, they force you to rethink your presentation. Simply repeating what you just said won't help someone who didn't get it the first time. You need to find a different way to communicate the idea. This not only reinforces the idea; but also opens your mind to connections between ideas that might not have been apparent under the original presentation. The more connected the knowledge, the easier it is to retain it.
The confluence of these is that, when preparing for a lecture, good professors will anticipate the areas where students stumble and think about alternate ways to present it. My strategy was generally to make my first explanation different than what was in the text. That way, if students had already read the text (no, I'm not naive enough to think that most students read the text before the lecture), they would already be on the second explanation. If not, and a question came up, I could always fall back on what was in the text. This meant that I had dual explanations for pretty much everything the course covered. That's a powerful set of knowledge.
So that's what I'm trying to do with these named results. I come across the result in the text, and I try to figure out how I would present it differently to a class being taught out of this text. Sure, it would be even better to actually teach the class, but I think this method is pretty effective. Of course, there's no substitute for practice, so I really do need to up the hours and work more problems as well.
Sunday, September 25, 2016
Failure of expectations
No, this has nothing to do with the expected value of a random variable, unless that random variable is one that describes whether I succeed at things. This is, after all, Sunday, so we're taking the day off from math.
Two weeks ago, I wrote that I thought I was mentally prepared for running Mark Twain. That, obviously was laughably wrong. Not only did I fold when the going got tough, I folded almost immediately. The time from the onset of real difficulties to the DNF was just over an hour; in the context of a 100; that's a pretty quick collapse.
So how was I that far off in my assessment of readiness? Honestly, I'm not entirely sure, but a few possible explanations come to mind:
Two weeks ago, I wrote that I thought I was mentally prepared for running Mark Twain. That, obviously was laughably wrong. Not only did I fold when the going got tough, I folded almost immediately. The time from the onset of real difficulties to the DNF was just over an hour; in the context of a 100; that's a pretty quick collapse.
So how was I that far off in my assessment of readiness? Honestly, I'm not entirely sure, but a few possible explanations come to mind:
- It's been a while (18 months) since I've done one of these and I forgot how hard they are.
- Lowering my goals made me less likely to fight for them because I didn't consider them worthy. This one has history on it's side. The only other running race I've ever DNF'd was also a 100 where I was just trying to finish. While I've never won a 100, I usually go into them thinking I should be competitive (and, I usually am).
- Looking bad in front of the local crowd was particularly discouraging. This is certainly true, but it's not like they've never seen me in trouble before. Furthermore, everyone was being genuinely supportive. Pride may well have had something to do with it, but that certainly wasn't the fault of circumstance.
I'm guess it's a combination of all three, but mostly 2. At any rate, I signed up to run the Tunnel Hill 100 in a few weeks to sort all this crap out. I can't go out to Leadville not being 100% sure that I can run a 100.
Saturday, September 24, 2016
Transformations on monotonic partitions
This one doesn't appear as a named result, though I found it in more than one text and it's pretty crucial for a lot of transformations.
Let X be a random variable with pdf fX(x). Let Y = g(x). If A0, ..., Ak are a partition of the sample space of X such that P(A0) = 0 and fX(x) is continuous on each Ai then if g(x) can be partitioned into g1(x), ..., gk(x) such that:
Then
&space;=&space;\left\{\begin{matrix}&space;\sum_{i=1}^k&space;f_X(g_i^{-1}(y))\left&space;|&space;\frac{d}{dy}g_i^{-1}(y)&space;\right&space;|&space;&&space;\quad&space;y&space;\in&space;g(\cup&space;A_i&space;)\\&space;0&space;&&space;\quad&space;\textup{otherwise}&space;\end{matrix}\right.)
OK, that's a mouthful, but if you can get past the details to see the result for what it is, the details are self-evident (except for the A0 partition, which doesn't carry any mass and is just a technical device that makes proving the theorem easier).
The transformation goes up and down, but you can chop it into bits where each bit just goes up or just goes down. Further, the projection of each bit is continuous and maps to the same range (this assumption can be generalized away, but it makes the formula more complicated). Finally, the inverse of each bit has a continuous derivative.
If all that is true, then the pdf of y is just the sum of each of the inverses times the absolute value of the inverse derivative.
Another way to think of it: at any point x, fX(x) is how much weight gets put on that point as X varies along the number line, In the simple monotone result from Wednesday, the transformed pdf, fY(y), is just inverse mapped back to that weight, fX(x), with a "speed adjustment" because Y is "moving" at a different speed than X as indicated by g. All that matters is the speed, not the direction, which is why the absolute value is necessary. In this result, we're saying the same thing except that multiple values of x map to the same y, so we have to add them all up, still adjusting for the speed differences at each point.
Let X be a random variable with pdf fX(x). Let Y = g(x). If A0, ..., Ak are a partition of the sample space of X such that P(A0) = 0 and fX(x) is continuous on each Ai then if g(x) can be partitioned into g1(x), ..., gk(x) such that:
- g(x) = gi(x) for all x in Ai
- each gi(x) is monotone on Ai
- gi(Ai) = gj(Aj) for all i, j (that is, the image of each partition is the same under g)
- each gi-1(y) has a continuous derivative on gi(Ai)
Then
OK, that's a mouthful, but if you can get past the details to see the result for what it is, the details are self-evident (except for the A0 partition, which doesn't carry any mass and is just a technical device that makes proving the theorem easier).
The transformation goes up and down, but you can chop it into bits where each bit just goes up or just goes down. Further, the projection of each bit is continuous and maps to the same range (this assumption can be generalized away, but it makes the formula more complicated). Finally, the inverse of each bit has a continuous derivative.
If all that is true, then the pdf of y is just the sum of each of the inverses times the absolute value of the inverse derivative.
Another way to think of it: at any point x, fX(x) is how much weight gets put on that point as X varies along the number line, In the simple monotone result from Wednesday, the transformed pdf, fY(y), is just inverse mapped back to that weight, fX(x), with a "speed adjustment" because Y is "moving" at a different speed than X as indicated by g. All that matters is the speed, not the direction, which is why the absolute value is necessary. In this result, we're saying the same thing except that multiple values of x map to the same y, so we have to add them all up, still adjusting for the speed differences at each point.
Friday, September 23, 2016
Lipschitz continuity and Banach's fixed-point theorem
I glossed over yesterday the conditions needed for differentiating under integration. The conditions aren't terribly interesting, but they do touch on an important result from Analysis. Lipschitz continuity is a strong form of continuity that, among other things, lets you swap derivatives and integrals. Note that it's actually stronger than needed for that, but also often easier to prove than the minimal condition.
Anyway, the definition is plain enough if you're comfortable with metric spaces. Just in case you're not, we'll start with the definition on the real number line with the standard euclidean distance (the absolute difference between two numbers):
One useful result is that if f maps a space to itself and K is less than 1, the function is called a contraction mapping and it can be shown that there exists a fixed point, that is, there exists x* in X such that f(x*) = x*. Intuitively this makes sense; if a function is squeezing a larger portion of the space into a smaller portion space across all values, there must be a point where it converges. The proof, originally from Banach in 1922, is less than intuitive, but really quite elegant. It's in any analysis text or online for those interested in looking it up.
Anyway, the definition is plain enough if you're comfortable with metric spaces. Just in case you're not, we'll start with the definition on the real number line with the standard euclidean distance (the absolute difference between two numbers):
If f(x) is a function from R to R, then f is Lipschitz continuous if there exists a constant K > 0 such that, for all x1, x2 in R, |f(x1) - f(x2)| < K|x1- x2|.Basically, this says that the slope of the graph can't get too crazy steep. The generalization to all metric spaces simply replaces the absolute values with whatever distance metric is being used for the space, that is:
If (X, dX) and (Y, dY) are metric spaces then f: X - Y is Lipschitz continuous if there exists K > 0 such that, for all x1, x2 in X, dY(f(x1), f(x2)) < KdX(x1, x2).This condition is rather independent of many other seemingly related conditions. For example, a function can be Lipschitz continuous and not be differentiable everywhere (e.g., |x|). Plenty of differentiable functions are not Lipschitz continuous (e.g., x2). Analytic functions may or may not be Lipschitz continuous. So, you have to check, is the bottom line.
One useful result is that if f maps a space to itself and K is less than 1, the function is called a contraction mapping and it can be shown that there exists a fixed point, that is, there exists x* in X such that f(x*) = x*. Intuitively this makes sense; if a function is squeezing a larger portion of the space into a smaller portion space across all values, there must be a point where it converges. The proof, originally from Banach in 1922, is less than intuitive, but really quite elegant. It's in any analysis text or online for those interested in looking it up.
Thursday, September 22, 2016
Moment Generating Functions
I'll be honest, I hate this topic. I can't tell you why. It always seems weird and contrived. But, it's also pretty foundational, so it needs to be noted.
The nth moment of a random variable X is E(Xn). The central moment is the same thing, except that you first norm the variable to it's mean, that is, E(X - E(X))n.
The moment generating function (mgf), is the function that, wait for it... generates the moments. You do this through successive differentiation, which immediately suggests that this is some function involving e. Indeed it is: MX(t) = E(etX). This function is only considered to be defined when the expectation exists in some neighborhood of 0.
To get the actual moments, you differentiate at zero. In the continuous case, you need to be able to move the differentiation inside the integral, which is not always valid, but is for pretty much any distribution a person would actually use. If your pdf is some sort of fractal function that can't be Riemann Integrated, you probably don't have a defined expectation at zero, anyway.
Since each differentiation of etX yeilds another power of X, we get
M(n)X(t) = E(XnetX), so M(n)X(0) = EXn
OK, fine, and there may be a few odd cases where computing the mgf and then differentiating is easier than just computing the moment directly (but not many). The real power of this exercise is that, for many distributions, the mgf uniquely identifies the distribution. So, if you don't know the distribution, but you can compute moments from a sample from the distribution, you may be able to take a decent stab at the underlying distribution.
Of course, us Bayesians would just put a non-parametric prior on there and let the likelihood point the way, but I suppose some would call that cheating.
The nth moment of a random variable X is E(Xn). The central moment is the same thing, except that you first norm the variable to it's mean, that is, E(X - E(X))n.
The moment generating function (mgf), is the function that, wait for it... generates the moments. You do this through successive differentiation, which immediately suggests that this is some function involving e. Indeed it is: MX(t) = E(etX). This function is only considered to be defined when the expectation exists in some neighborhood of 0.
To get the actual moments, you differentiate at zero. In the continuous case, you need to be able to move the differentiation inside the integral, which is not always valid, but is for pretty much any distribution a person would actually use. If your pdf is some sort of fractal function that can't be Riemann Integrated, you probably don't have a defined expectation at zero, anyway.
Since each differentiation of etX yeilds another power of X, we get
M(n)X(t) = E(XnetX), so M(n)X(0) = EXn
OK, fine, and there may be a few odd cases where computing the mgf and then differentiating is easier than just computing the moment directly (but not many). The real power of this exercise is that, for many distributions, the mgf uniquely identifies the distribution. So, if you don't know the distribution, but you can compute moments from a sample from the distribution, you may be able to take a decent stab at the underlying distribution.
Of course, us Bayesians would just put a non-parametric prior on there and let the likelihood point the way, but I suppose some would call that cheating.
Wednesday, September 21, 2016
Transforming a pdf.
This is another unnamed result, but it seems pretty useful.
Let X be a random variable and Y = g(X) then
If the g-1(y) has a continuous derivative when g-1(y) is in the support of X, then it immediately follows that:
fY(y) = fX(g-1(y)) |d/dy g-1(y)| for all y in the support of Y (and zero elsewhere).
This can make quick work of useful, but otherwise non-trivial, transformations like the Inverted Gamma and Square of a Normal (which is Chi-squared with 1 degree of freedom).
Let X be a random variable and Y = g(X) then
- if g is a strictly increasing function on the support of X then FY(y) = FX(g-1(y)) for y in the support of Y. (The support of a continuous random variable is the set of values where the density function is greater than zero).
- if g is a strictly decreasing function on the support of X then FY(y) = 1 - FX(g-1(y))
If the g-1(y) has a continuous derivative when g-1(y) is in the support of X, then it immediately follows that:
fY(y) = fX(g-1(y)) |d/dy g-1(y)| for all y in the support of Y (and zero elsewhere).
This can make quick work of useful, but otherwise non-trivial, transformations like the Inverted Gamma and Square of a Normal (which is Chi-squared with 1 degree of freedom).
Tuesday, September 20, 2016
CDF
Another basic one today as I want to spend more time working problems than writing.
A Cumulative Distribution Functions (cdf), F(x) for a random variable X is defined as F(x) = P(X ≤ x). From this definition and the basic axioms, we get a few noteworthy properties:
A Cumulative Distribution Functions (cdf), F(x) for a random variable X is defined as F(x) = P(X ≤ x). From this definition and the basic axioms, we get a few noteworthy properties:
- F(x) is a monotonically increasing function of x (using National Institute of Standards and Technology definition which allows the function to be flat in spots; some authors would call this non-decreasing).
- limx→ -∞ F(x) = 0 and limx→∞ F(x) = 1
- F(x) is right-continuous, that is for all x0, limx↓x0 F(x) = F(x0)
Monday, September 19, 2016
Overcomplicating things (Bayes' Rule)
At the outset of this "Identify all named results" adventure, I mentioned that I already knew Bayes' Rule. I should hope so. It generally pops up in chapter 1 of any introductory probability text. I am surprised, however, by how often authors make it more complicated than it has to be.
First, the rule: P(A|B) = P(B|A)P(A) / P(B).
The easy way to remember it is to include the identity used to derive it:
P(A|B)P(B) = P(A ∩ B) = P(B|A)P(A)
Then just eliminate the middle term and divide by P(B). Done. Easy.
So why complicate it? For some reason, a lot of texts want to list what they call a "more general" result based on partitioning the sample space S into {Ai} (meaning, the subsets Ai are mutually exclusive and their union equals S). Then, the rule is re-written:
&space;=&space;\frac{P(B|A_i)P(A_i)}{\sum_j&space;P(B|A_j)P(A_j)})
OK, that's certainly true, but how is it more "general"? There's nothing about that equation that requires Ai to be in the partition. It could be any set and the equation still holds. Adding constraints makes a formula less general, not more, so let's drop the subscript and just call the event of interest A:
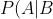&space;=&space;\frac{P(B|A)P(A)}{\sum_j&space;P(B|A_j)P(A_j)})
Now, let's look at the denominator. Remember the original identity: P(B|A)P(A) = P(A ∩ B). Also recall that, if the sets are mutually exclusive, the sum of the probabilities is the probability of the union. Combine that with the basic associative properties of countable unions and intersections to get:
P(A_j)&space;&=&space;\sum_j&space;P(A_j&space;\cap&space;B)\\&space;&=&space;P(\cup_j&space;\{A_j&space;\cap&space;B\})&space;\\&space;&=&space;P(\{\cup_j&space;A_j\}&space;\cap&space;B)&space;\\&space;&=&space;P(S&space;\cap&space;B)&space;=&space;P(B)&space;\end{align*})
Which brings us back to the denominator of the original equation. Sure, if you have a partitioned space, feel free to substitute it in, but that makes it a special case of the theorem. The simple version is the general case.
One could, of course, argue that the simple version is just the partitioned version where the partitions are simply A and Ac. That's still a bit lame, as the denominator is messier than it needs to be and, again, that partitioning is buying you absolutely nothing up top. If computing the denominator is easier when done by partitions, go for it, but that is simply a computational substitution, not a generalization of the result. The numerator is the same no matter how you label it.
First, the rule: P(A|B) = P(B|A)P(A) / P(B).
The easy way to remember it is to include the identity used to derive it:
P(A|B)P(B) = P(A ∩ B) = P(B|A)P(A)
Then just eliminate the middle term and divide by P(B). Done. Easy.
So why complicate it? For some reason, a lot of texts want to list what they call a "more general" result based on partitioning the sample space S into {Ai} (meaning, the subsets Ai are mutually exclusive and their union equals S). Then, the rule is re-written:
OK, that's certainly true, but how is it more "general"? There's nothing about that equation that requires Ai to be in the partition. It could be any set and the equation still holds. Adding constraints makes a formula less general, not more, so let's drop the subscript and just call the event of interest A:
Now, let's look at the denominator. Remember the original identity: P(B|A)P(A) = P(A ∩ B). Also recall that, if the sets are mutually exclusive, the sum of the probabilities is the probability of the union. Combine that with the basic associative properties of countable unions and intersections to get:
Which brings us back to the denominator of the original equation. Sure, if you have a partitioned space, feel free to substitute it in, but that makes it a special case of the theorem. The simple version is the general case.
One could, of course, argue that the simple version is just the partitioned version where the partitions are simply A and Ac. That's still a bit lame, as the denominator is messier than it needs to be and, again, that partitioning is buying you absolutely nothing up top. If computing the denominator is easier when done by partitions, go for it, but that is simply a computational substitution, not a generalization of the result. The numerator is the same no matter how you label it.
Sunday, September 18, 2016
No redemption
Well, that was a bust.
At the Mark Twain 100, which was supposed to salvage at least a little redemption from this weekend, I got caught up in trying to win the damn thing rather than simply finish it. Problem is, I'm just not that good any more. As a result, I flamed out and didn't accomplish either. (It was fun to run in the lead in the second half of a 100, though, first time I've done that.)
The actual cause of the collapse is easy enough to identify. After a well-paced first lap (of four), I failed to appreciate how much the midday heat was a problem on the second and didn't make the needed adjustment. I knew I was going deep, but thought that it would be fine for just a few hours and the cooler temps of the night would save me. Well, I folded before that happened.
Far more distressing was the speed of the collapse. I noticed that heat was an issue early in lap 2, but didn't really make much in the way of adjustment. I was still running OK and when some clouds moved in, I covered miles 40-50 well enough move myself essentially into a tie for the lead (the top four were all in the aid station together between laps 2 & 3). I was second back on the trail and, while I was backing off from the first two laps, still felt like I was running well. When I actually caught the leader at mile 55, my body shut down almost immediately.
What this tells me is that my brain hasn't quite caught up to the fact that I'm not a 100-mile per week runner anymore and don't have the reserves to survive mid-race surges. My body was going way further into a hole than my brain realized and, as soon as I caught the lead and stopped pressing, my body took over and turned everything off as quickly as possible.
The next few miles were pretty miserable and I finally packed it in.
I don't regret trying to win the race. That's what you do in races. I'm not particularly bothered by coming up short. Even World Champions lose. I am very bothered by the fact that what I think I can do and what I'm actually capable of are so out of sync. That's going to result in a lot of very unsatisfying races.
Unless, of course, I come to my senses and stop racing. That really is the answer. This whole take care of your family while working a stressful job and getting a PhD is not the ideal setting for competitive running. Running is my daily meditation and I don't think ditching it altogether would be a very good idea. However, there's no reason to be stressing of results. The activity will have to be good enough on it's own for at least the duration of my studies.
At the Mark Twain 100, which was supposed to salvage at least a little redemption from this weekend, I got caught up in trying to win the damn thing rather than simply finish it. Problem is, I'm just not that good any more. As a result, I flamed out and didn't accomplish either. (It was fun to run in the lead in the second half of a 100, though, first time I've done that.)
The actual cause of the collapse is easy enough to identify. After a well-paced first lap (of four), I failed to appreciate how much the midday heat was a problem on the second and didn't make the needed adjustment. I knew I was going deep, but thought that it would be fine for just a few hours and the cooler temps of the night would save me. Well, I folded before that happened.
Far more distressing was the speed of the collapse. I noticed that heat was an issue early in lap 2, but didn't really make much in the way of adjustment. I was still running OK and when some clouds moved in, I covered miles 40-50 well enough move myself essentially into a tie for the lead (the top four were all in the aid station together between laps 2 & 3). I was second back on the trail and, while I was backing off from the first two laps, still felt like I was running well. When I actually caught the leader at mile 55, my body shut down almost immediately.
What this tells me is that my brain hasn't quite caught up to the fact that I'm not a 100-mile per week runner anymore and don't have the reserves to survive mid-race surges. My body was going way further into a hole than my brain realized and, as soon as I caught the lead and stopped pressing, my body took over and turned everything off as quickly as possible.
The next few miles were pretty miserable and I finally packed it in.
I don't regret trying to win the race. That's what you do in races. I'm not particularly bothered by coming up short. Even World Champions lose. I am very bothered by the fact that what I think I can do and what I'm actually capable of are so out of sync. That's going to result in a lot of very unsatisfying races.
Unless, of course, I come to my senses and stop racing. That really is the answer. This whole take care of your family while working a stressful job and getting a PhD is not the ideal setting for competitive running. Running is my daily meditation and I don't think ditching it altogether would be a very good idea. However, there's no reason to be stressing of results. The activity will have to be good enough on it's own for at least the duration of my studies.
Friday, September 16, 2016
Bonferroni and Boole
In it's simplest form, Bonferroni's inequality states:
P(A ∩ B) ≥ P(A) + P(B) - 1
This result is both self-evident and largely useless. The self-evident part comes from the fact that
1 ≥ P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
Just flip the 1 and the P(A ∩ B) to the other sides of the inequality.
The largely useless part comes from the fact that, unless A and B are pretty likely, the bound is negative and any probability is lower-bounded by a negative number.
Still, it's a named result. So I have dutifully logged it.
However, while that's what gets mentioned in most basic probability courses, there's more to it than that. The Bonferroni bound actually applies to any number of sets and, as the number of sets goes up, the number of terms increases, giving a convergent sequence of upper and lower bounds.
Boole's Inequality states that P(∪Ai) ≤ ∑P(Ai) for countable unions of {Ai}. This can be proved fairly readily either with or without induction directly from the Borel and Kolmogorov axioms. Bonferroni built a framework which started with that result as a special case, but then, by considering successively complex intersections, created general upper and lower bounds for finite unions that converge to equality.
Let
,\quad&space;S_2&space;=&space;\sum_{1\le&space;i&space;<&space;j\le&space;n}^nP(A_i&space;\cap&space;A_j))
and, in general
)
Basically, Sk is the sum of the probabilities of all intersections of k sets from {Ai}. Then, for odd k we have an upper bound on the union:
&space;\le&space;\sum^k&space;(-1)^{j-1}S_j)
and for even k we get a lower bound:
&space;\ge&space;\sum^k&space;(-1)^{j-1}S_j)
Note that when k = 1, we have Boole's inequality and when k = n, equality holds giving us the inclusion-exclusion principle. Going back to n = 2, we get the following two bounds:
k = 1: P(A ∪ B) ≤ P(A) + P(B) Boole's inequality.
k = 2: P(A ∪ B) = P(A) + P(B) - P(A ∩ B) Exclusion-inclusion principal on two sets.
Combine them and you get the silly result quoted up top. As noted, for small values of n, this is something that can be easily worked out by hand without a unifying formula. However, the fact that it generalizes to any value of n, including countably infinite sets, and the bounds always converge to equality makes it an elegant statement of a significant and less than obvious result. I think texts should stop attributing the n = 2 result to Bonferroni. It makes him look like a total fraud when he actually did some pretty fine work.
P(A ∩ B) ≥ P(A) + P(B) - 1
This result is both self-evident and largely useless. The self-evident part comes from the fact that
1 ≥ P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
Just flip the 1 and the P(A ∩ B) to the other sides of the inequality.
The largely useless part comes from the fact that, unless A and B are pretty likely, the bound is negative and any probability is lower-bounded by a negative number.
Still, it's a named result. So I have dutifully logged it.
However, while that's what gets mentioned in most basic probability courses, there's more to it than that. The Bonferroni bound actually applies to any number of sets and, as the number of sets goes up, the number of terms increases, giving a convergent sequence of upper and lower bounds.
Boole's Inequality states that P(∪Ai) ≤ ∑P(Ai) for countable unions of {Ai}. This can be proved fairly readily either with or without induction directly from the Borel and Kolmogorov axioms. Bonferroni built a framework which started with that result as a special case, but then, by considering successively complex intersections, created general upper and lower bounds for finite unions that converge to equality.
Let
and, in general
Basically, Sk is the sum of the probabilities of all intersections of k sets from {Ai}. Then, for odd k we have an upper bound on the union:
and for even k we get a lower bound:
Note that when k = 1, we have Boole's inequality and when k = n, equality holds giving us the inclusion-exclusion principle. Going back to n = 2, we get the following two bounds:
k = 1: P(A ∪ B) ≤ P(A) + P(B) Boole's inequality.
k = 2: P(A ∪ B) = P(A) + P(B) - P(A ∩ B) Exclusion-inclusion principal on two sets.
Combine them and you get the silly result quoted up top. As noted, for small values of n, this is something that can be easily worked out by hand without a unifying formula. However, the fact that it generalizes to any value of n, including countably infinite sets, and the bounds always converge to equality makes it an elegant statement of a significant and less than obvious result. I think texts should stop attributing the n = 2 result to Bonferroni. It makes him look like a total fraud when he actually did some pretty fine work.
Thursday, September 15, 2016
Borel Sets and Kolmogorov Axioms
This is really foundational, but a foundation is a good place to start building. To define probabilities, we need something to define them on. Such structures are known by two names: sigma algebras and Borel sets. If S is a set, then a family of subsets of S is a Borel set if:
- The empty set is included.
- The family is closed under complements (which, combined with #1, means that the full set S is also included).
- The family is closed under countable unions (which, with #2 and DeMorgan's Laws, implies it's also closed under countable intersections).
In the case where S is finite or countably infinite, the most obvious Borel set is the set of all subsets of S. When S is uncountable (for example, the real number line), things get a bit stickier. Fortunately, most probability questions are interested in ranges of the real line, so a Borel set that includes all intervals of the form [a, b], [a, b), (a, b], and (a, b) does nicely.
The point of defining the Borel set B for a sample space is that we can then define a measure P that maps the Borel set to [0,1]. To be a probability measure, P needs to meet the Kolmogorov Axioms:
- P(A) ≥ 0 for all A ∈ B.
- P(S) = 1.
- if A1, ..., An ∈ B are pairwise disjoint, then P(∪Ai) = ∑P(Ai)
Obviously, any finite measure P on B can be converted to a probability measure by simply norming it to 1. That is, if P is a measure on B and P(S) is finite, then P'(A) = P(A) / P(S) is a probability measure on B. This fact turns out to be extremely useful in Bayesian statistics since the marginal likelihood is often difficult to compute but, as long as we know it's finite, we can often ignore it and then norm the resulting posterior after the fact.
Wednesday, September 14, 2016
Cauchy-Schwarz Inequality
I'm pivoting over to stats results, and what better result to use for that than Cauchy-Schwarz? It's ostensibly a Linear Algebra result, but the application to stats is both elegant and significant.
First, the result.
Given two vectors u, v from an inner product space V, the following inequality holds:
|<u, v>|2 ≤ <u, u> <v, v> (equivalently, |<u, v>| ≤ ||u|| ||v||) with equality holding if and only if u and v are linearly dependent (that includes the case where one or both is 0)
In the case of the real-valued plane with the Euclidean distance metric, this becomes the familiar triangle inequality: the shortest distance between two points is a straight line; going through any point off the line makes the journey longer.
In the case of less obvious spaces, the result is less obvious, but it means the same thing. If you want to get somewhere, head in that direction. OK, fine, but what does this have to do with statistics?
Let X and Y be random variables. Define the inner product as <X, Y> = E(XY). Then
|E(XY)|2 < E(X2) E(Y2)
Transform X' = X - E(X) and Y' = Y - E(Y) and you have
|Cov(X, Y)|2 = |E(X'Y')|2 ≤ E(X'2) E(Y'2) = Var(X) Var(Y)
which is an important result. Given Cauchy-Schwarz, the proof is simply showing that E(XY) really is an inner product, which is pretty straightforward. Thus, while it's really a special case, many stats texts will list Cov(X, Y)2 ≤ Var(X) Var(Y) as the Cauchy-Schwarz inequality.
First, the result.
Given two vectors u, v from an inner product space V, the following inequality holds:
|<u, v>|2 ≤ <u, u> <v, v> (equivalently, |<u, v>| ≤ ||u|| ||v||) with equality holding if and only if u and v are linearly dependent (that includes the case where one or both is 0)
In the case of the real-valued plane with the Euclidean distance metric, this becomes the familiar triangle inequality: the shortest distance between two points is a straight line; going through any point off the line makes the journey longer.
In the case of less obvious spaces, the result is less obvious, but it means the same thing. If you want to get somewhere, head in that direction. OK, fine, but what does this have to do with statistics?
Let X and Y be random variables. Define the inner product as <X, Y> = E(XY). Then
|E(XY)|2 < E(X2) E(Y2)
Transform X' = X - E(X) and Y' = Y - E(Y) and you have
|Cov(X, Y)|2 = |E(X'Y')|2 ≤ E(X'2) E(Y'2) = Var(X) Var(Y)
which is an important result. Given Cauchy-Schwarz, the proof is simply showing that E(XY) really is an inner product, which is pretty straightforward. Thus, while it's really a special case, many stats texts will list Cov(X, Y)2 ≤ Var(X) Var(Y) as the Cauchy-Schwarz inequality.
Tuesday, September 13, 2016
QR Factorization
Let's jump right to the result:
If A is a real valued n x n matrix, then A can be written as QR where Q is an orthogonal matrix (that is, the columns of Q are orthogonal unit vectors) and R is an upper triangular matrix. If A is invertible, then the factorization is unique if we require the diagonal elements of R to be positive.
A bit of a mouthful, but intuitive enough in light of yesterday's result. First lets look at the case when A is invertible. If that's so, then A is of rank n, which means its columns span Rn. Now, from yesterday, that means we not only can create an orthonormal basis from the columns of A, but we know how to do it in a way that each of the original columns is a linear combination of the basis elements that precede it. That is:

Thus, A = QR where Q contains the unit vectors from the Gram-Schmidt process and R = {rij} are the coefficients of those vectors to construct the original set of columns in A. Since rij = 0 for all i > j, R is upper triangular.
In the case where A is not invertible, the rank of A is less than n, so just run Gram-Schmidt and whenever you hit a column that is dependent on the previous columns, stick a zero vector in A and just set the coefficients in R to reconstruct the original column from the existing basis rows. You'll still wind up with an upper-triangular R since you can just stick any non-zero coefficient you want in the remaining part of that row of R (which is why R is only guaranteed unique if A is invertible).
Decomposing a matrix like this is useful for solving least squares problems as well as certain eigenvalue problems. The rub is that the Gram Schmidt process is numerically unstable so, while it's a great way to explain why this works, it's not a very good way to actually get a solution. Fortunately, there are numerically stable alternatives that are included in any computation package. The value of Gram-Schmidt is simply that it does such a good job of illustrating how this all works.
If A is a real valued n x n matrix, then A can be written as QR where Q is an orthogonal matrix (that is, the columns of Q are orthogonal unit vectors) and R is an upper triangular matrix. If A is invertible, then the factorization is unique if we require the diagonal elements of R to be positive.
A bit of a mouthful, but intuitive enough in light of yesterday's result. First lets look at the case when A is invertible. If that's so, then A is of rank n, which means its columns span Rn. Now, from yesterday, that means we not only can create an orthonormal basis from the columns of A, but we know how to do it in a way that each of the original columns is a linear combination of the basis elements that precede it. That is:
Thus, A = QR where Q contains the unit vectors from the Gram-Schmidt process and R = {rij} are the coefficients of those vectors to construct the original set of columns in A. Since rij = 0 for all i > j, R is upper triangular.
In the case where A is not invertible, the rank of A is less than n, so just run Gram-Schmidt and whenever you hit a column that is dependent on the previous columns, stick a zero vector in A and just set the coefficients in R to reconstruct the original column from the existing basis rows. You'll still wind up with an upper-triangular R since you can just stick any non-zero coefficient you want in the remaining part of that row of R (which is why R is only guaranteed unique if A is invertible).
Decomposing a matrix like this is useful for solving least squares problems as well as certain eigenvalue problems. The rub is that the Gram Schmidt process is numerically unstable so, while it's a great way to explain why this works, it's not a very good way to actually get a solution. Fortunately, there are numerically stable alternatives that are included in any computation package. The value of Gram-Schmidt is simply that it does such a good job of illustrating how this all works.
Monday, September 12, 2016
Gram-Schmidt orthogonalization
Given that any inner product space has an orthonormal basis, the obvious question is, "How do I find one?" It's actually pretty easy. The Gram-Schmidt process starts with any set of vectors that span the space and sequentially converts them into an orthonormal basis.
The process starts by picking any one of the vectors and normalizing it (that is, dividing it by it's length so the resulting vector has the same direction, but length 1). Then, you take another vector, and compute it's projection onto the space spanned by the first vector. The difference between the two is necessarily orthogonal to the first space. Normalize that, and you've got your next basis vector. Keep going until you've reached the dimension of the space. (Every text I've checked starts with a basis rather than simply a set of vectors that span the space, but there's no reason for that restriction as long as you chuck the dependent vectors as you go and stop when you've reached the dimension of the space).
Formally, the process is as follows:
Let {xi} span an inner product space V of dimension n.
Let u1 = x1/||x1||
for 0 < k < n, if xk+1 is in the space spanned by {ui} i ≤ k, then drop xi from the set and renumber the remaining vectors (this somewhat ugly step is why the textbooks like to start with a basis rather than a spanning set. Repeat until you have an xk+1 independent from {ui} i ≤ k.
Let uk = (xk+1 - pk) / ||xk+1 - pk|| where

Then {ui} is an orthonormal basis of V.
While slick in it's own right, the real power of this is evident when we look at the factorization of matrices. Tune in tomorrow for more linear algebra excitement!
The process starts by picking any one of the vectors and normalizing it (that is, dividing it by it's length so the resulting vector has the same direction, but length 1). Then, you take another vector, and compute it's projection onto the space spanned by the first vector. The difference between the two is necessarily orthogonal to the first space. Normalize that, and you've got your next basis vector. Keep going until you've reached the dimension of the space. (Every text I've checked starts with a basis rather than simply a set of vectors that span the space, but there's no reason for that restriction as long as you chuck the dependent vectors as you go and stop when you've reached the dimension of the space).
Formally, the process is as follows:
Let {xi} span an inner product space V of dimension n.
Let u1 = x1/||x1||
for 0 < k < n, if xk+1 is in the space spanned by {ui} i ≤ k, then drop xi from the set and renumber the remaining vectors (this somewhat ugly step is why the textbooks like to start with a basis rather than a spanning set. Repeat until you have an xk+1 independent from {ui} i ≤ k.
Let uk = (xk+1 - pk) / ||xk+1 - pk|| where
Then {ui} is an orthonormal basis of V.
While slick in it's own right, the real power of this is evident when we look at the factorization of matrices. Tune in tomorrow for more linear algebra excitement!
Sunday, September 11, 2016
Prepping for 100
It's Sunday, so I'm not studying today (though I will have to tend to some work items this evening). Having failed at preparing for the Q, I thought I'd write a bit about preparing for the other half of my "redemption weekend" coming up.
In many ways, running a 100-mile race is a lot like taking the Q - you can't prep at the last minute and expect to succeed. Just as it takes years of schooling to acquire the breadth and depth of knowledge to get past the Q, running a 100 is something rarely even attempted by a newbie, much less completed (as with all things in life, there are exceptions).
There are two typical progressions. The most common is to first develop fitness as a road runner; perhaps even some serious marathoning. Then, usually in one's 30's or 40's when improvements in speed are hard to come by but endurance is still improving, there's some dabbling in longer distances often accompanied by a move to trails as the preferred surface. One doesn't have to hang with the ultra crowd for very long to understand that, while they are an accepting bunch, to really be in the club, you have to run a hundred. Actually doing so usually follows pretty soon after that or never happens at all.
The other entrance is from other sports that demand similar endurance such as 24-hour orienteering, adventure racing, and full length ironman triathlons, People from these backgrounds already get the mental discipline; they just need to get their bodies able to run for that long. People from these backgrounds are less likely to "work up" to the 100-mile distance. Often, the 100 is the first ultra-distance run they ever do (though, in fairness, adventure racers and 24-hour orienteers will often cover 60-80 miles on foot in the context of their events, so they've technically already done a bunch of ultras).
One could say I took both paths. I ran a lot as a kid. Not competitively; I just loved to run. I'm not talking about the usual running around playing games with other kids. I was running 40-50 miles a week in my early teens. I did a fair number of running races in my 20's, but my real competitive focus was on my cycling. At age 30, I ran my first marathon (which didn't go very well) and, at 33, ran another (which did). About a year after that, I started running mostly trails and became a charter member of the St. Louis Ultrarunners Group (SLUGs). While I enjoyed running with them and did do a few training runs over 26.2 miles, I didn't run my first official ultra until I was 42. It was a 12-hour event and I ran 100K. My first 100 mile race didn't come for another 5 years.
The reason for the relatively slow progression on the first path is that I was simultaneously taking the second. Along with the switch to trails, I was also getting involved in both adventure racing and 24-hour orienteering (I also dabbled in triathlons, but decided that addressing my incompetence in the water was going to be more work than it was worth). So, when I ran that first ultra, I had already run several events of 24 hours or more. The distance really wasn't intimidating at all. I didn't rush to be "in the club" because I really didn't care to be. The SLUGs liked me and I liked them. That was enough.
I'm not really sure what prompted me to run that first 100-miler. I guess I just felt it was time to do it. I made a few mistakes, but it basically went pretty well. I finished 6th in a field of around 200. My second 100 was a bit of a disaster, though you wouldn't know it from the finish position (10th). Just about everybody went to pieces that day as it was crazy hot. After that race I started thinking about how to really prepare for a hundred.
Here's what I've come up with, both from my own experiences and from talking to many top 100-milers:
In many ways, running a 100-mile race is a lot like taking the Q - you can't prep at the last minute and expect to succeed. Just as it takes years of schooling to acquire the breadth and depth of knowledge to get past the Q, running a 100 is something rarely even attempted by a newbie, much less completed (as with all things in life, there are exceptions).
There are two typical progressions. The most common is to first develop fitness as a road runner; perhaps even some serious marathoning. Then, usually in one's 30's or 40's when improvements in speed are hard to come by but endurance is still improving, there's some dabbling in longer distances often accompanied by a move to trails as the preferred surface. One doesn't have to hang with the ultra crowd for very long to understand that, while they are an accepting bunch, to really be in the club, you have to run a hundred. Actually doing so usually follows pretty soon after that or never happens at all.
The other entrance is from other sports that demand similar endurance such as 24-hour orienteering, adventure racing, and full length ironman triathlons, People from these backgrounds already get the mental discipline; they just need to get their bodies able to run for that long. People from these backgrounds are less likely to "work up" to the 100-mile distance. Often, the 100 is the first ultra-distance run they ever do (though, in fairness, adventure racers and 24-hour orienteers will often cover 60-80 miles on foot in the context of their events, so they've technically already done a bunch of ultras).
One could say I took both paths. I ran a lot as a kid. Not competitively; I just loved to run. I'm not talking about the usual running around playing games with other kids. I was running 40-50 miles a week in my early teens. I did a fair number of running races in my 20's, but my real competitive focus was on my cycling. At age 30, I ran my first marathon (which didn't go very well) and, at 33, ran another (which did). About a year after that, I started running mostly trails and became a charter member of the St. Louis Ultrarunners Group (SLUGs). While I enjoyed running with them and did do a few training runs over 26.2 miles, I didn't run my first official ultra until I was 42. It was a 12-hour event and I ran 100K. My first 100 mile race didn't come for another 5 years.
The reason for the relatively slow progression on the first path is that I was simultaneously taking the second. Along with the switch to trails, I was also getting involved in both adventure racing and 24-hour orienteering (I also dabbled in triathlons, but decided that addressing my incompetence in the water was going to be more work than it was worth). So, when I ran that first ultra, I had already run several events of 24 hours or more. The distance really wasn't intimidating at all. I didn't rush to be "in the club" because I really didn't care to be. The SLUGs liked me and I liked them. That was enough.
I'm not really sure what prompted me to run that first 100-miler. I guess I just felt it was time to do it. I made a few mistakes, but it basically went pretty well. I finished 6th in a field of around 200. My second 100 was a bit of a disaster, though you wouldn't know it from the finish position (10th). Just about everybody went to pieces that day as it was crazy hot. After that race I started thinking about how to really prepare for a hundred.
Here's what I've come up with, both from my own experiences and from talking to many top 100-milers:
- First and foremost, it's not a physical competition as much as a mental one. Everybody wants to stop at some point during a hundred. Some do, some simply slow to a crawl, some find a way to keep making good progress. Physical ability does not predict how people get sorted into those three groups. But the first group always loses and the second generally finishes well behind the third (even if they were well ahead at the time of crisis). Therefore, the most important preparation is developing an absolute steely resolve that you WILL NOT QUIT. Note that this is not at all the same thing as "getting tough". Getting tough is often counterproductive in an ultra. You need to realize when you need recovery and figure out how to get it. Trying to push through a bad patch only makes it that much worse. However, you must absolutely convince yourself that bad patches are nothing more than temporary conditions from which you will extricate yourself. You must never lose the hope that you will be running well again and seize the opportunity to do so as soon as it is presented.
- That said, it is still really hard physically. Therefore, the best physical preparation I have found is that which is used for the toughest race distance of them all: the marathon. Note that I said toughest "race distance", not distance. I can jog a marathon any day of the week. Racing one is the hardest thing I've ever done. I don't know anyone who's ever run a marathon well who says otherwise. Good marathon training is more than adequate physical prep for running a hundred. Again, there's more in that sentence than may be obvious. The Runner's World "You can run a marathon on 35 miles a week" program is not good marathon training. It may well get you to the finish line of a marathon, but you certainly won't run it well. And, it won't get you to the finish of a 100 at all. Good marathon training is at least 60 miles a week. Most serious marathoners are between 80 and 100. I seem to do best averaging just below 100 with a few weeks in the 110-120 mile range sprinkled in. Also, good marathon training includes a fair bit of "quality" work such as tempo runs and even some intervals. I use Daniel's approach which stipulates two structured workouts a week and the rest just gets filled in with base mileage as your schedule allows.
- Assuming that at least part of the distance will be on trail, it makes sense to get in a fair bit of trail running. I try to get on a technical trail at least once a week. That's been harder to do since going back to school. Fortunately, 20 years of trail running counts for a lot and my technique may be somewhat dulled, but it's still sound.
- Assuming that you're not one of the elites who finishes before sunset, you also need to practice running at night. It's not simply running with a flashlight. There are lots of little adjustments that need to be made. If you have to think about them, you'll fall, because your brain isn't very good at thinking during the last few hours of a hundred.
And, really, that's about it. It's not complicated. But, that doesn't make it easy.
So, where does that leave me for Mark Twain 100 next weekend? First point is no problem. I've done enough of these that I know what I'm getting into and I'm ready to deal with stuff as it comes. Second point is a lot more dicey. The last marathon I really trained for was Milwaukee a year ago. Prep for The Woodlands last spring was not terrible, but it wasn't great either. I've had plenty of long runs since then, including the Silver Rush 50 a couple months ago. The quality workouts have been rather sparse. If I was trying to win this one, I'd say I'm way underprepared. Since I'm just trying to finish it in under 24 hours (which will get me the pretty 2-tone belt buckle), I'm probably OK.
Last month featured a decent amount of technical trail and a few night runs. Again, not good enough for a full-on competitive effort, but probably adequate given the reduced goals.
Of course, if I do find myself in good competitive shape going into the late stages, I'll give it my best shot. I'm just not counting on that.
Saturday, September 10, 2016
Cramer's Rule
Here's a significantly more useful result from Linear Algebra:
Let A be a non-singular n x n matrix and b an n-dimensional real vector.
Let Ai be A with the ith column replaced with b.
If x is a unique solution to Ax = b, then xi = |Ai| / |A|
Well, useful in the Q-question world where n < 4. After that, taking the determinants gets to be an awful lot of work and you're back to busting out a numerical package.
Let A be a non-singular n x n matrix and b an n-dimensional real vector.
Let Ai be A with the ith column replaced with b.
If x is a unique solution to Ax = b, then xi = |Ai| / |A|
Well, useful in the Q-question world where n < 4. After that, taking the determinants gets to be an awful lot of work and you're back to busting out a numerical package.
Friday, September 9, 2016
Wronskian
Following yesterday's intention to catalog named results, let's start with a weird one.
If we have n functions that are n-1 times differentiable on an interval [a,b], the Wronskian is defined as:
 = \begin{vmatrix} f_1(x) & ... & f_n(x) \\ f'_1(x) & ... & f'_n(x) \\ ... & ... & ... \\ f^{(n-1)}_1(x) & ... & f^{(n-1)}_n(x) \end{vmatrix}](http://latex.codecogs.com/gif.latex?W[f_1,&space;...,&space;f_n](x)&space;=&space;\begin{vmatrix}&space;f_1(x)&space;&&space;...&space;&&space;f_n(x)&space;\\&space;f'_1(x)&space;&&space;...&space;&&space;f'_n(x)&space;\\&space;...&space;&&space;...&space;&&space;...&space;\\&space;f^{(n-1)}_1(x)&space;&&space;...&space;&&space;f^{(n-1)}_n(x)&space;\end{vmatrix})
So, basically, you create a matrix where each column vector is the successive derivatives of fi and you take the determinant.
The significance is the following theorem:
If there exists x in [a,b] such that W[f1, ..., fn](x) ≠ 0, then f1, ..., fn are linearly independent.
Why does that matter? Well, it means they form a basis for the subspace they span, which is sometimes a useful thing to know. (At least, it's useful if you're staring at a Q question that asks you to find the basis of a subspace. Maybe not that useful any other time.)
Apparently, it's also occasionally useful for solving higher order systems of differential equations, though the methods I dug up on line didn't seem a whole lot easier than just solving the equations the normal way. At any rate, not too many people do that anymore. Numerical packages are so powerful now, it's just not worth the effort except in trivial cases. Wronski developed this idea in 1812, a decade before Babbage secured funding for building the world's first computer.
So, probably won't be using this result very much unless it comes up on the Q, which it might.
I should probably also remember that the converse is not necessarily true. You can have independent functions with a Wronskian that is zero everywhere.
If we have n functions that are n-1 times differentiable on an interval [a,b], the Wronskian is defined as:
So, basically, you create a matrix where each column vector is the successive derivatives of fi and you take the determinant.
The significance is the following theorem:
If there exists x in [a,b] such that W[f1, ..., fn](x) ≠ 0, then f1, ..., fn are linearly independent.
Why does that matter? Well, it means they form a basis for the subspace they span, which is sometimes a useful thing to know. (At least, it's useful if you're staring at a Q question that asks you to find the basis of a subspace. Maybe not that useful any other time.)
Apparently, it's also occasionally useful for solving higher order systems of differential equations, though the methods I dug up on line didn't seem a whole lot easier than just solving the equations the normal way. At any rate, not too many people do that anymore. Numerical packages are so powerful now, it's just not worth the effort except in trivial cases. Wronski developed this idea in 1812, a decade before Babbage secured funding for building the world's first computer.
So, probably won't be using this result very much unless it comes up on the Q, which it might.
I should probably also remember that the converse is not necessarily true. You can have independent functions with a Wronskian that is zero everywhere.
Thursday, September 8, 2016
Foundation
I've recently come to what should have been a pretty obvious realization. I guess I've known it for some time, but prepping for the Q has brought it more into focus.
Important results get named. Not necessarily after the person who derived or invented them, but named just the same. Minor results just get listed in texts as Theorem 4.3.2 or something like that. Major results may still be listed that way, but then there will be a parenthetic attribution like (Bayes' Rule). I hadn't given much thought to this until I started looking things up on the web. Since a web page discussing some technicality can't waste space deriving all the necessary supporting results, they have to be able to say "By Bayes' Rule, it follows that ..." and so on. This, of course, is not new to the web, academic papers have been doing the same thing for centuries. I just haven't read too many of those in the past 25 years.
Anyway, my point is that it's a great way to quickly go through a text and find all the important results. So, that's what I'm going to do. Over the next few weeks, I'm going to catalog every named result in all the texts I'm studying from. By completely committing those to memory, I'll not only have the foundational results I need for proving results on the Q, I'll also be in a much better spot for discussing thesis points with other faculty.
And, by the way, Bayes' Rule: P(X|Y) = P(Y|X)P(X)/P(Y). I knew that one already.
Important results get named. Not necessarily after the person who derived or invented them, but named just the same. Minor results just get listed in texts as Theorem 4.3.2 or something like that. Major results may still be listed that way, but then there will be a parenthetic attribution like (Bayes' Rule). I hadn't given much thought to this until I started looking things up on the web. Since a web page discussing some technicality can't waste space deriving all the necessary supporting results, they have to be able to say "By Bayes' Rule, it follows that ..." and so on. This, of course, is not new to the web, academic papers have been doing the same thing for centuries. I just haven't read too many of those in the past 25 years.
Anyway, my point is that it's a great way to quickly go through a text and find all the important results. So, that's what I'm going to do. Over the next few weeks, I'm going to catalog every named result in all the texts I'm studying from. By completely committing those to memory, I'll not only have the foundational results I need for proving results on the Q, I'll also be in a much better spot for discussing thesis points with other faculty.
And, by the way, Bayes' Rule: P(X|Y) = P(Y|X)P(X)/P(Y). I knew that one already.
Wednesday, September 7, 2016
Reset
Well, I threw in the towel. Work isn't letting up and the Q is only 9 days away. I deferred it to next semester. While I was at it, I also dropped the Cloud Computing course since if I don't carve out some serious study time, I'm going to be right back in this same bind four months from now.
So, this is a pretty big reset. It probably means I won't finish in three years. I always thought that was ambitious, but it seemed doable up until now. I still wouldn't say it's out of the question, but certainly a lot less likely.
That may not be an entirely bad thing. A year ago, I just wanted to get my "union card" and move on. I figured that anybody hiring a new prof in his mid-50's wasn't going to care about the dissertation; they wanted the 30 years of work experience. The PhD was just one of those things you have to do to be in the club.
I still think that's true, but now I want the dissertation to matter. I've enjoyed digging into a topic. I want to do something of substance. That's not going to happen if my primary goal is to get through as quickly as possible. My remaining class is a directed study with my adviser. I'm hoping we really hone in on a productive line of research this fall. I'd like to come out of UMSL with 3-4 publications along with the thesis. From what I can tell, success in academics isn't that much different from success in anything else. Sure, talent counts, but what really matters is that you're willing to do the work. I am.
So, this is a pretty big reset. It probably means I won't finish in three years. I always thought that was ambitious, but it seemed doable up until now. I still wouldn't say it's out of the question, but certainly a lot less likely.
That may not be an entirely bad thing. A year ago, I just wanted to get my "union card" and move on. I figured that anybody hiring a new prof in his mid-50's wasn't going to care about the dissertation; they wanted the 30 years of work experience. The PhD was just one of those things you have to do to be in the club.
I still think that's true, but now I want the dissertation to matter. I've enjoyed digging into a topic. I want to do something of substance. That's not going to happen if my primary goal is to get through as quickly as possible. My remaining class is a directed study with my adviser. I'm hoping we really hone in on a productive line of research this fall. I'd like to come out of UMSL with 3-4 publications along with the thesis. From what I can tell, success in academics isn't that much different from success in anything else. Sure, talent counts, but what really matters is that you're willing to do the work. I am.
Tuesday, September 6, 2016
Some things are going great
If a little pessimism has crept into my posts over the last few weeks, it's because I really did want to put the Q behind me. Actually, that's an understatement. I wanted to crush it and use that result to get the best faculty members on my committee en route to a dissertation of some consequence.
Well, that may still happen, but only if I wait until February to take it. Work has simply been overwhelming and, even if I am able to pass the exam in ten days, it would be "as one escaping through the flames" as the apostle Paul so aptly put it.
However, that work thing has not been entirely one-sided. Yes, it's pretty much destroyed my life in the short term, but that's pretty much the nature of IT work. The only way to distinguish yourself in this field is by being willing to drop everything when the situation calls for it. And, the situation has called for it. As a result, I've scored some pretty big wins at the office:
Well, that may still happen, but only if I wait until February to take it. Work has simply been overwhelming and, even if I am able to pass the exam in ten days, it would be "as one escaping through the flames" as the apostle Paul so aptly put it.
However, that work thing has not been entirely one-sided. Yes, it's pretty much destroyed my life in the short term, but that's pretty much the nature of IT work. The only way to distinguish yourself in this field is by being willing to drop everything when the situation calls for it. And, the situation has called for it. As a result, I've scored some pretty big wins at the office:
- Our annual summer release (always our most stressful) went without incident.
- A month after go-live, we've had no significant production issues. I did have to work two weekends (the final nails in the Q prep coffin) to work through some data quality issues, but those were problems at the source, not with our stuff.
- We closed our second successful iteration (of two) on the project to rehost all our reporting to a scalable platform (Hadoop/Impala/AtScale).
- Primarily as a result of the last item, the members of my team are begging to stay rather than be transferred off. We normally rotate assignments so people don't get burned out, but the developers are really eager to move onto the new technology stack.
So, even if it does knock me down a rung at school, the last couple months have certainly improved my standing at work. I was doing pretty well on both fronts coming into the summer. It will be easier to repair damage on the school side.
Monday, September 5, 2016
Less than hoped for
Today, I tried a dry run of the Q. I don't have an actual practice test, but I do have a list of questions that are supposed to be representative.
It didn't go well.
It's not that I didn't know what was being asked or what approach to take. It's just that all the little details that one needs to fill in the steps come so slowly (and sometimes, they escape me altogether). It's the difference between being familiar with the subjects and really knowing them. The only way I know to bridge that gap is lots of drill. With only ten days to go, that's not really an option.
Thursday, September 1, 2016
Sufficiently believable
Hey, here's something we haven't seen much of lately: a post about math. Yes, that is still my major and I haven't dropped out. That said, I'm pursuing a Philosopher's Doctorate, thus, rather than actually do any math, I'm just going to talk about it.
I was reviewing data reduction today and was struck by the tortured definition of a sufficient statistic: If T(X) is a sufficient statistic for θ, then any inference about theta should depend on the sample X only through the value T(X). That is, if x and y are two sample points such that T(x) = T(y), then the inference about θ should be the same whether X = x or X = y is observed.
Ok, the authors do give a formal definition that is more concise, but it still reflects this mentality that the world is this objective rules-based machine and we simply need to discover those rules. I don't know any theoretical physicists who believe that (and, yes, I do know several theoretical physicists; they aren't as rare as you might think). But the stats community, which serves primarily the empirical sciences (I'll be generous and include the social sciences in that group) where everything is debatable, still clings to this notion of absolute truth.
Of course, there are plenty of stats folks who don't. They're called Bayesians. Rather than get wrapped up around what θ is (or if it even exists), a Bayesian is only interested in what we believe about θ. A statistic is sufficient for θ if it fully informs our belief. That is, if our posterior belief about θ is the same whether we're given the statistic or the entire sample, then the statistic is sufficient.
The formal definitions drive this home.
Frequentist: A statistic T(X) is a sufficient statistic for θ if P(X|T(X)) does not depend on θ.
Baked into that is the notion of absolute truth. Otherwise, conditioning X on a function of itself makes no sense at all.
Bayesian: A statistic T(X) is a sufficient statistic for θ if P(θ|T(X)) = P(θ|X).
It's a fair debate, but it seems to me that if θ is the thing you care about but don't know, talking about sufficiency in terms of how much more you know after observing the statistic makes a lot more sense.
Just to be clear, Bayesians and frequentists don't actually disagree on what constitutes a sufficient statistic. The two definitions are equivalent. The disagreement is over what a sufficient (or any other) statistic actually tells you about the world.
I was reviewing data reduction today and was struck by the tortured definition of a sufficient statistic: If T(X) is a sufficient statistic for θ, then any inference about theta should depend on the sample X only through the value T(X). That is, if x and y are two sample points such that T(x) = T(y), then the inference about θ should be the same whether X = x or X = y is observed.
Ok, the authors do give a formal definition that is more concise, but it still reflects this mentality that the world is this objective rules-based machine and we simply need to discover those rules. I don't know any theoretical physicists who believe that (and, yes, I do know several theoretical physicists; they aren't as rare as you might think). But the stats community, which serves primarily the empirical sciences (I'll be generous and include the social sciences in that group) where everything is debatable, still clings to this notion of absolute truth.
Of course, there are plenty of stats folks who don't. They're called Bayesians. Rather than get wrapped up around what θ is (or if it even exists), a Bayesian is only interested in what we believe about θ. A statistic is sufficient for θ if it fully informs our belief. That is, if our posterior belief about θ is the same whether we're given the statistic or the entire sample, then the statistic is sufficient.
The formal definitions drive this home.
Frequentist: A statistic T(X) is a sufficient statistic for θ if P(X|T(X)) does not depend on θ.
Baked into that is the notion of absolute truth. Otherwise, conditioning X on a function of itself makes no sense at all.
Bayesian: A statistic T(X) is a sufficient statistic for θ if P(θ|T(X)) = P(θ|X).
It's a fair debate, but it seems to me that if θ is the thing you care about but don't know, talking about sufficiency in terms of how much more you know after observing the statistic makes a lot more sense.
Just to be clear, Bayesians and frequentists don't actually disagree on what constitutes a sufficient statistic. The two definitions are equivalent. The disagreement is over what a sufficient (or any other) statistic actually tells you about the world.
Subscribe to:
Posts (Atom)